目前看的GNN論文的一些總結

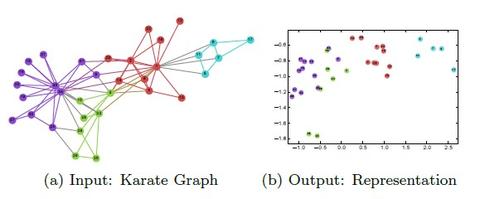
最近組會輪到我講了，打算講一下目前看的一些GNN論文以及該方向的一些重要思想，其中有借鑑論文[1]、[2]的一些觀點和《深入淺出圖神經網絡：GNN原理解析》一書中的觀點。其中可能有一些不準確和不全面的地方，歡迎大家指出。

1.爲什麼我們需要圖神經網絡：

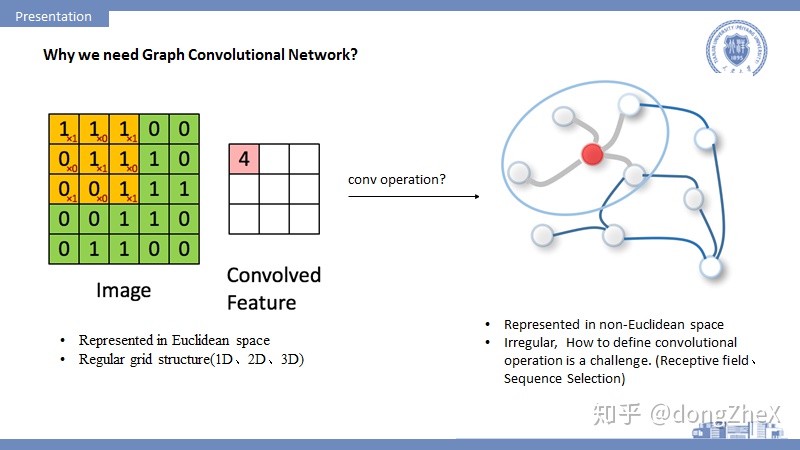
當前，深度學習技術已經在語音識別、機器翻譯、圖像分析和計算機視覺等方向取得了重要成果，之所以CNN、RNN等模型能夠在圖像、音頻等處理中取得很好地效果，其一個重要原因是：圖像、音頻等數據都可以很好地在歐氏空間中進行表示，並且以規則的柵欄結構呈現，CNN等可以很自然的在這些數據上進行操作。

而也有很多數據，如社交網絡數據、生物化學圖結構和引文網絡等，這些只能在非歐空間中表示，圖（Graph）是其中一個典型的表示方式。

圖結構數據的表示一般是不規則，傳統的CNN等模型無法直接運用在圖數據上，所以需要在圖上重新定義卷積操作。其中要着重考慮感受野如何定義，節點的順序性如何定義，如何進行池化操作等等，這方面大家可以參考論文論文[3]，其中有比較詳細的討論。

2.圖神經網絡發展的一些歷史

①最早的圖神經網絡是Network Embedding的形式，它的核心思想是通過表徵學習的方式，在保持當前空間一些幾何特性的前提下，把數據轉換到一個低維的、更加有判別能力的空間。常見的方法有LLE、DeepWalk、SNE、Graph Factorization等方法。更多可以參考，這篇知乎（謝謝該作者）：

蘇一：圖嵌入（Graph embedding）綜述​ zhuanlan.zhihu.com

這方面強烈建議看一下DeepWalk這篇論文，是network embedding中非常重的一篇論文，該方法借鑑NLP的思想，使用random walk和SkipGram來提取社交網絡數據中的結構信息。

這些方法的通病是對那些擁有節點特徵的數據不感冒，有些方法加入節點特徵的處理，但其實效果都不是特別好。

②在之後出現了Recurrent graph neural networks，這種方法的主要思想是假設一個節點不斷地與鄰居節點交換信息直到達到一個平衡，其大多借鑑了LSTM、GRU這些RNN模型，然後改進並運用到 圖數據上，這方面我沒有具體看過論文。大家如果有興趣可以參考論文[1]，然後再去查看相關論文。

③在2013年nips上，論文[4]提出使用圖信號處理技術來定義譜圖卷積，其核心思想是通過圖傅里葉變換將圖信號從空間域轉換到頻域，進而在頻域上定義圖卷積操作，其具體操作可以可以參考這篇知乎：

如何理解 Graph Convolutional Network（GCN）？​ www.zhihu.com

我們直接看結果：

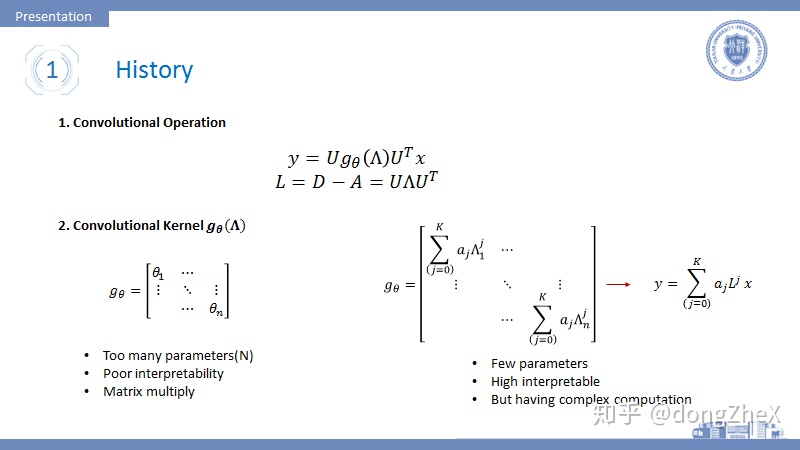
圖 3 上方的第一行式子就是對圖數據x進行的譜圖卷積操作，其中U代表拉普拉斯矩陣的特徵向量，Lambda表示拉普拉斯矩陣的特徵值矩陣，拉普拉斯矩陣是對稱矩陣，所以他一定可以進行對角化。

表示圖卷積的卷積核，最初始的卷積覈定義有兩種形式

1. 第一種爲圖3左下角形式爲一個擁有N（節點數）個參數的對角陣，這種形式比較簡單，但是會遇到幾個問題：（i）參數數量與圖節點數量掛鉤，在處理大圖時會產生參數過多的問題（ii）解釋性極差;（iii）需要計算特徵向量，並進行多次矩陣乘法，計算複雜度高。
2. 爲了解決1中的問題，提出了第二種圖3右下角的形式，這種形式看似複雜，但是可以通過對角化性質進行化簡成：

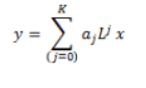
這是式子中，對於每個K只有一個參數，L的j次冪可以表示節點的j階連通性，這也帶來了較好的解釋性：中心節點聚合其K階鄰居的信息，所以K可以理解爲感受野，且參數數量等於K（一般K很小，例如K=2）。但是這個卷積核形式帶來一些問題如：需要計算L的冪，造成了較高的計算複雜度。

自此GNN變得可以一邊提取結構特徵、一邊提取節點特徵。

3. Basic Model

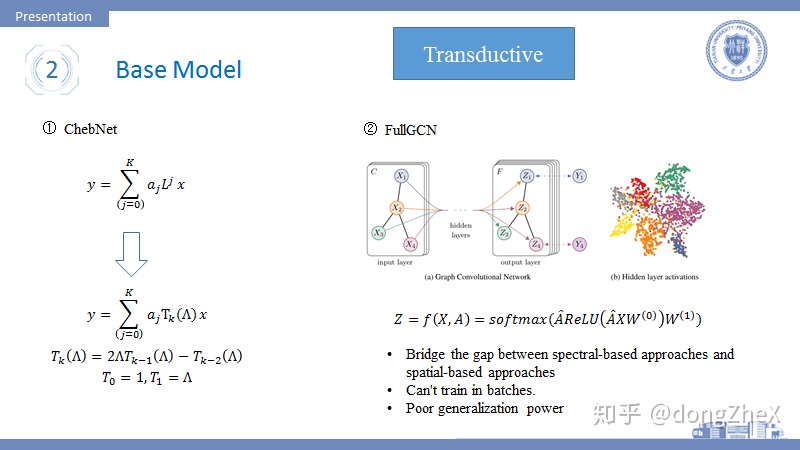
論文[5]提出了ChebNet（圖4左側），該模型對於圖卷積的改進在於使用切比雪夫多項式來近似計算拉普拉斯矩陣的冪運算，原來的冪運算可以通過遞歸的形式來求得，簡化了運算。

論文[6]是圖卷積領域一篇非常經典的論文，將圖卷積應用於半監督學習中。我們這裏不討論其半監督學習的方法。該論文在論文[5]的基礎上進行了一階近似，即每次卷積操作只對節點的一階鄰居進行信息聚合，並且省略了部分參數。除此之外，作者在層與層之間加入了線性變化矩陣和激活函數的操作，並使用softmax和交叉熵損失完成節點分類任務。圖4右側展示了模型的核心計算公式，可以看到卷積核幾乎消失了。論文[1]中也因此稱該論文爲連接譜圖卷積和空間域卷積的橋樑。除此之外，該式中的 爲經過標準化和增加自連接的拉普拉斯矩陣，可以起到穩定計算的作用。具體細節可以查詢具體論文。

值得一提的是，從半監督的角度來看這篇論文，也可以解釋爲使用圖卷積提取結構信息來達到使用少量標籤數據完成節點分類任務的目的。但是這篇論文在半監督上做的並不是特別好，我在做實驗的時候發現模型對於標籤數據的依賴性還是很大的，當減少訓練集的標籤數據時，模型效果會明顯的下降。所以現在半監督領域有許多改進CN的工作，想辦法用更少的標籤來訓練GCN，這些論文一個通常的特徵就是做實驗的時候會擺出訓練集的分割比。

目前提到的方法存在着很多問題：

• 無法進行分批訓練，其原因是的存在，無法對分批的數據完成運算，這也對應了該方法的靈活性差，無法處理大圖。
• 模型基於transductive，即在訓練過程中，測試集的數據也有參與，這造成模型的泛化能力很差。
• 無法通過加深網絡層數來加強網絡，這是GNN領域的一個重要問題。Shallow or Deep？這方面在文末會順帶一提，相關論文也非常之多。

基於以上前兩個兩個比較致命的缺點，研究者使用空間域卷積來解決。空間域卷積的論文也比較多：DCNN(擴散卷積)、GraphSage、GAT(基於self-attention)、LGCN(鄰居採樣+top-k selection+ 1DCNN)等等，其實後面講的模型都是空間域卷積，有比較有代表性的模型即GraphSAGE：

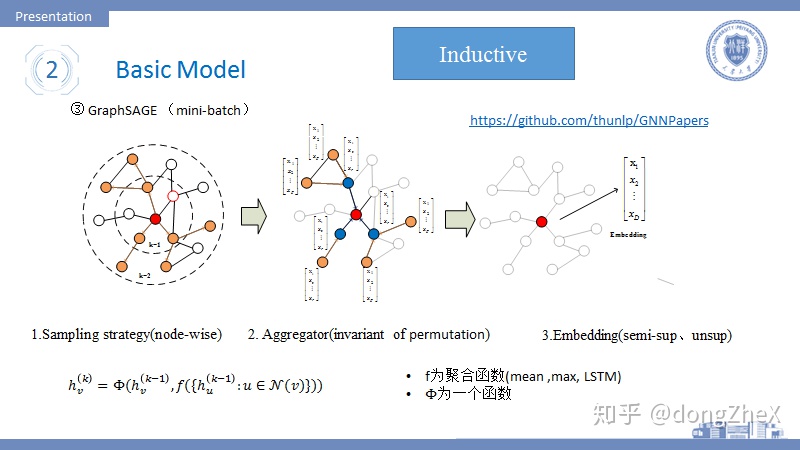
該模型指出，以前的模型的目標是爲每個不同的節點學習到一個唯一的Embedding，這導致模型的可擴展性很差。本論文[7]提出GraphSAGE將目標定於學習聚合器，聚合器的任務在於完成鄰居節點的信息聚合，因此GraphSAGE不會因爲新節點的加入而造成模型無法工作。除此之外，GraphSAGE支持分批訓練。

如圖5，該模型的工作步驟可以分爲：

• 分批採樣若干源節點，對於其中一箇中心節點來說，首先對其一階鄰居採樣固定數目個節點，若感受野爲2，則在對中心節點的每個一階鄰居的鄰居節點進行固定數目的採樣，採樣數目爲超參數。一般感受野的大小K=2.
• 採樣結束後，對節點的鄰居節點進行聚合，其聚合方式應該具有排列不變性，作者提供了三種：（i）mean，（ii）max, （iii）lstm，其中mean的聚合方式讓模型近似等價於論文[6]，lstm不具有排列不變性。
• 中心節點的K階鄰域聚合完畢後，通過concat或sum的形式兩者進行融合，獲得最後的embdding，然後用於半監督學習或者無監督學習。

其分批算法流程可以表示爲：

具體的算法細節，大家可以參考源碼，這篇論文十分適合落地。

值得一提，這篇論文也存在着一定的缺陷，後面會提到。

下面在分別講一下幾個重要的研究方向，分類可能不太對，大家湊活着看。

3. Analysis

論文[8]提出了一種描述GNN的通用框架即信息傳遞機制。其核心思想很簡單，通過中心節點、其一個鄰接節點和它們之間的邊信息生成一個信息M，然後將中心節點能生成的所有信息加和得到m，然後將該信息傳遞給中心節點做一個融合得到新的Embedding。若是做圖分類任務，則再加入一個Readout層來做一個全局的池化。其實這種思想在論文[9]中也有提高過。

作者認爲大家的模型都應該按照他的框架來，紅紅火火恍恍惚惚紅紅火火\(^o^)/~。

在通用框架方面，還有非常多的代表性論文，Relational Inductive Biases, Deep Learning, and Graph Networks.arxiv 2018.paper，這篇論文中也提出了非常多的框架。

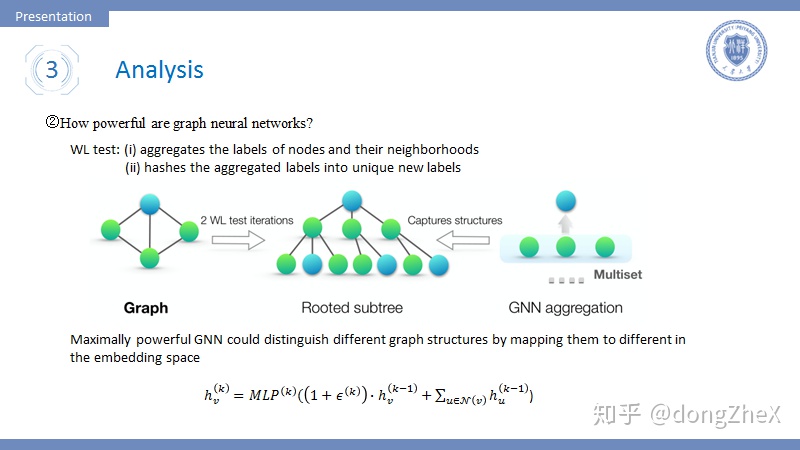
論文[10]探討了什麼樣的模型能夠有更強大的表達能力。早在GraphSAGE中，作者就提出了空間域卷積的操作與Weisfeiler-Lehman test十分相似, WL test的流程如下：

1. 聚合節點的節點與他們鄰居節點的標籤。
2. 對聚合結束後的新標籤進行hash操作。
3. 迭代1、2幾次，觀察標籤的分佈來判斷圖是否同構。

如圖8中間的圖所示，GNN的聚合和WL test都能得到一個類似樹的結構，作者認爲擁有不同子樹的根節點應該擁有不同的Embedding。

這就引出了作者的一個理論：

簡單一點說，聚合函數f、 、readout的函數映射是單射的。

作者據此，設計了一種能夠發揮最大表達能力的模型，即圖8最下方的模型。該模型聚合函數使用了加和（作者在論文中對比了mean、max和sum的優劣），使用了MLP，readout使用了跨層級的加和操作。

論文[11] 探討了強大的圖神經網絡的必要性問題，作者在文中去除了那些複雜的聚合操作，之加入一些線性變化和激活函數，在readout層使用MLP來增強網絡。

網絡的輸入數據有進行更改，其數據位節點度、節點信息，節點K接鄰居信息的concat結果，可以認爲作者僅僅通過在輸入數據中加入度信息和鄰居信息，而用線性變化和激活函數代替鄰域節點聚合操作仍能在圖分類任務上取得很好地效果。（後面有篇論文特別強調了度信息的重要性）。從這點看來，圖神經網絡應該是什麼樣的還處於混沌狀態。我們怎麼才能更加有效地、更加高效率的獲取數據中的結構信息呢。

4 Efficiency

圖神經網絡領域還有一個關於模型效率的方向。

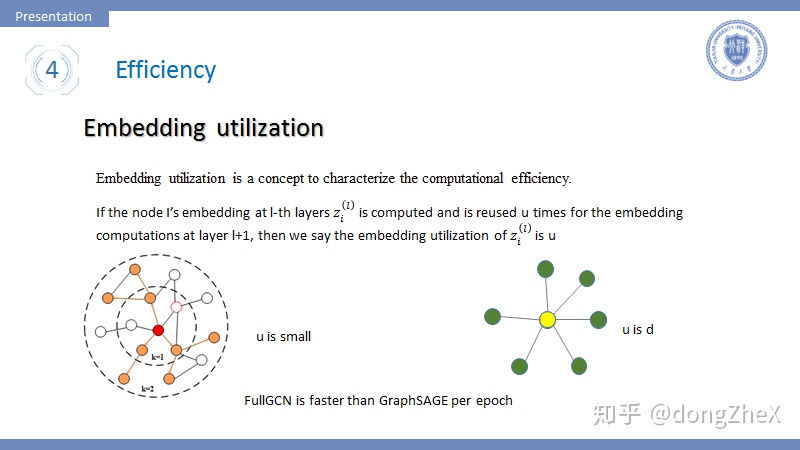
首先引入一個概念Embedding utilization，該概念最早提出在論文[12]中。如果一個節點在l層中被採樣計算，並且在l+1層重複利用u次，我們說節點利用率爲u。這個指標可以很好地衡量模型的時間複雜度，embedding utilization跟採樣圖中邊數量成正比。

這裏說一個事實，雖然GraphSAGE採用了分批訓練極大地提升了模型的的收斂速度，但是其每個epoch的時間卻比FullGCN[6]要慢很多，這用Embedding utilization可以很好地解釋。

可以很容易的想到，在GraphSAGE中的u是很小的，這一層採樣的節點在下一層也被採樣的機率是不大的。而對於FullGCN這種全採樣的方法，u是節點度的平均值，很明顯要大於GraphSAGE，所以GraphSAGE的per-epoch time要更長。

接下來介紹幾種重要的採樣方式：

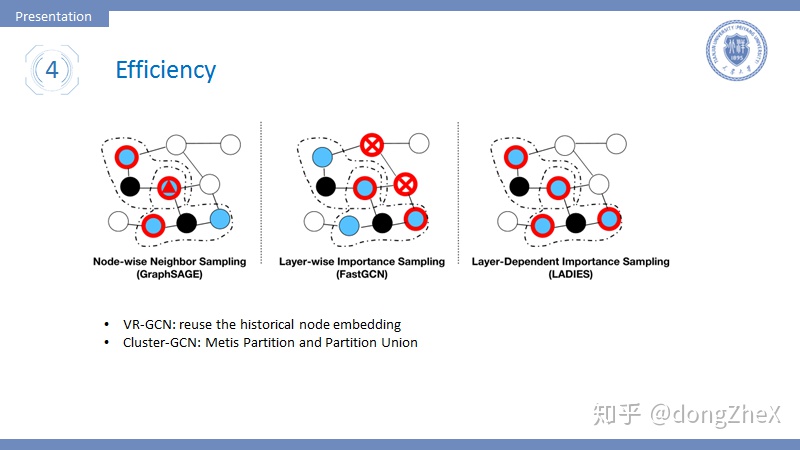
1. Node-wise：其代表就是GraphSAGE，每次採樣中心節點固定數目的鄰居節點，這種方法面臨的問題是，當網絡層數變深時，模型的複雜程度指數增加。
2. Layer-wise：該方法進行層間獨立採樣，在每一層中都單獨採樣固定數目的節點，這樣就不會有指數級的複雜度，並且採樣遵循重要性採樣方法（具體見論文[13]、[14]）。這種方法面臨的問題是，節點間的關係可能很稀疏，導致模型的效果下降。
3. Layer-wise x Node-wise: 論文[15]提出一種方法，在層間獨立採樣的基礎上，在第一層採樣固定數目節點，然後下一層的採樣在第一層所有節點的鄰居節點中採樣固定數目節點，這樣可以同時減少複雜度、減弱稀疏。
4. 基於圖劃分：論文[15]提出了一種基於圖劃分的方式，首先使用METIS劃分算法對圖進行劃分，劃分結果趨向於擁有更多的邊，然後在這個圖劃分中完成圖卷積操作可以有效提升節點利用率。有一個問題，劃分之間的關係很可能損失掉，這會導致模型性能下降，作者採用將多個劃分合併的方法來減弱這種趨勢。

這個研究領域的成果其實並不是具體的模型，而是一種訓練方法，這是需要注意的。

5.Pooling

對應於傳統深度學習中的pooling，GNN中也有池化操作，這方面我看的論文不是很多，簡單介紹一下。Pooling常用於圖分類任務中。

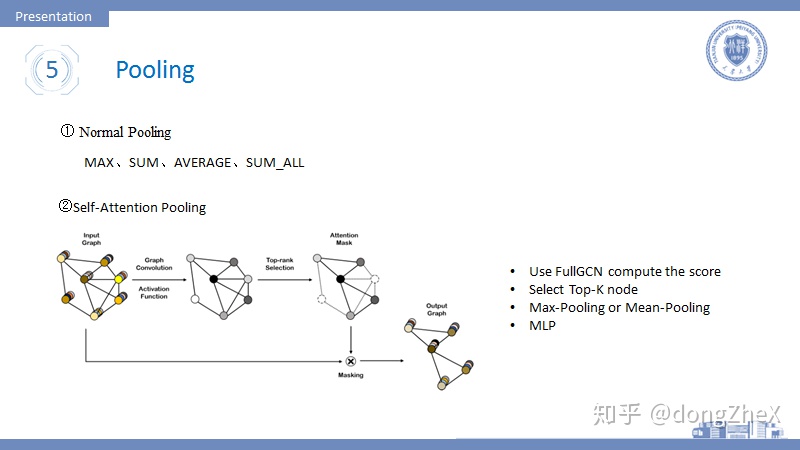
Pooling常用於readout中進行全局池化，最基本的方法有Max-pooling、SUM-pooling、mean-pooling等。

論文[16]首次將attention加入到pooling操作中（在這之前有GAT網絡用於圖卷積，大家有興趣可以查看相關論文）。該方法的步驟如下：

1. 使用FullGCN進行操作得到每個節點的一個Embedding。
2. 根據Embedding計算top-k節點，然後刪除剩餘節點。
3. 將top-k進行Max-pooling、Mean-pooling進行池化，在用MLP進行映射進而完成圖分類任務。

作者在論文中給出了兩種模型搭建方式，可分別應用於大圖數據和小圖數據中，具體大家可以參考論文。

這裏說一下attention的問題，attention最近在GNN領域的應用非常多，比較有代表性的就是GAT這個模型，具體的大家可以看論文。這裏我想說一下我理解的attention在GNN中作用：一是幫助結構特徵的提取，幫助我們得知哪個鄰居更加重要，需要更大的權重。二是幫助構造節點序列，在CNN中卷積核中心節點的周圍節點都因爲相對位置而獲得順序，但是圖節點的鄰居並沒有順序，這時候通過attention機制可以幫助我們搞定節點順序選擇問題。attention我覺得可以作爲一個小trick用到各種模型中來加強模型效果。

有研究者發現，目前的pooling方法沒有類似於傳統pool的層級結構，論文[19]就此提出了DiffPool模型。

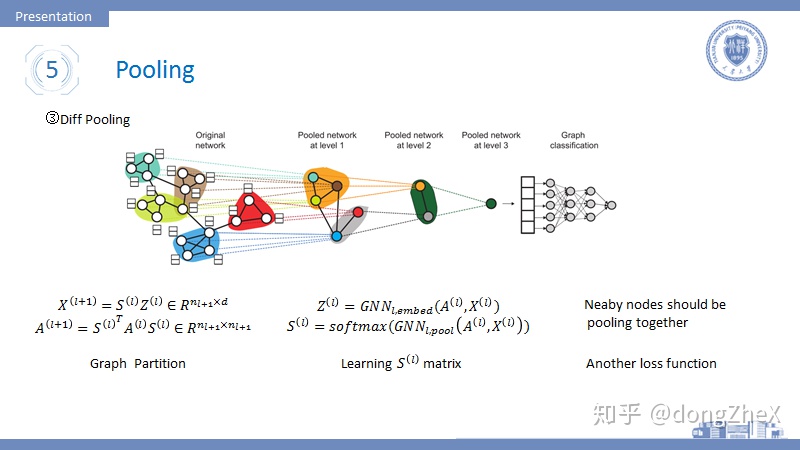
模型的思想是這樣的，在模型的前向傳播過程中，加入一個矩陣S，S的作用是將當前層的節點進行劃分，劃分後節點的數目減少，在網絡的最後劃分數目變爲1。其計算過程如圖14左側所示，更加具體的操作細節，可以參考論文原文。

這個S如何獲得呢，答案是通過學習獲得。模型被分爲兩部分，一部分學習節點的embedding，一部分用於學習矩陣S（其中用到了top-k的思想），其計算模型如圖14中間所示。

作者在訓練過程中，發現模型很難收斂，遂加入一個新的損失項，該損失基於假設：鄰居節點應該儘可能的被分在同一個劃分中。

6.About Experiment

看這方面論文很驚悚，讓我感覺以前的實驗真的白做了。

論文[18]做了這樣一個工作，他在一個統一的實驗設置下，對當前重要的模型進行測試。

論文指出現今的模型存在一個問題，他們的實驗設置非常不同，不同的實驗導致會導致模型效果天差地別，並且缺少可再現性。。最近自己在做實驗的時候也深有體會，無論如何也無法復現一些論文中的效果，增加訓練集節點數目會讓效果天差地別。

作者將模型評價分爲兩個階段：（i）model selection （ii） model assessment。前者爲超參數的選擇階段，後者爲模型結果測試階段。一個合格的評價流程可以提高模型的可再現性。

就此作者提出了一套基於交叉驗證的評測流程，如圖15所示。

除此之外，我還得知了並非所有的數據都有節點特徵，像如reddit這樣的社交網絡數據是缺少節點特徵的，論文采用的方法是將節點特徵設置爲相同值或者度的獨熱編碼。

論文在完成測試後，得到兩個重要結論：

1. 一些沒有適用結構特徵提取的方法在某些情境下，效果優於GNN，所以這告訴我們當前的GNN模型沒有充分提取結構信息。
2. 節點的度是一個非常重要的特徵，能夠顯著提升模型效果，這也印證了之前的GFN模型。

現在在圖神經網絡領域還缺少一個像ImageNet這樣的評測平臺，不可否認的是ImageNet對於計算機視覺的發展推動十分大。所以我們需要這樣一個平臺。

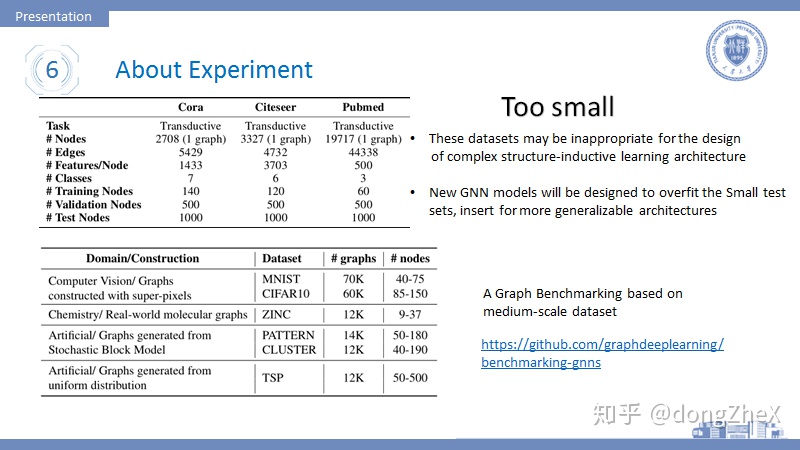
論文[19]做了一個benchmark。

該論文指出當前工作常用的引文網絡數據集存在很大的問題，它的數據規模太小了，這對於開發更加複雜的圖神經網絡模型是十分不利的。一些好的模型會在這些數據集上趨向於過擬合而不是提升泛化能力。

所以作者在計算機視覺、生物信息、社交網絡等領域建立了多箇中等規模的數據集，並使用一致的評測流程來保證公平，希望這個benchmark可以促進圖神經網絡的發展。

7.GNN領域中的一些問題：

1. 訓練方式問題（sampling）：目的是尋找一種訓練方式，使得收斂速度加快、time per epoch時間降低，並且不明顯損耗效果。值得一提VR-GCN在重要性採樣這一方面已經做到了方差爲0，很不錯了。
2. Deep network : GNN現在一般的層數爲2-3層，研究者發現加深網絡會導致模型的效果變差。我理解的有以下幾種解釋方法：（1）拉普拉斯矩陣的冪運算在指數很大時， 變化很小。（2）GCN它基於假設：讓相鄰的節點儘可能的處於同一類，如果加深層數會導致距離比較遠（不屬於同一類）的節點成爲同類，這明顯會損耗GNN效果。（3）當GNN的層數加深，會聚集更多節點的noise information。（4）當GNN層數加深時，中心節點的節點特徵會慢慢地被丟棄，所以有工作通過加多個自旋的方式來加深層數。（5）統計學常識：參數越多，需要的數據越多，然而沒有大型圖數據集。解決加深GNN層數的問題主要使用skip connection的方法，如殘差網絡，hightway network,Dilated 等方法。
3. 異質圖：異質圖中的節點和邊擁有不同的類型，異質圖問題一般很複雜，現在也有很多相關的工作，其中一個重要思想是先想辦法將節點和邊分類，然後進行類內的信息聚合，然後在進行類間的節點聚合。
4. 有向圖：前面提到的很多GNN模型只面向無向圖，要想處理有向圖，就必須考慮child和father這一項信息。
5. 動態圖：圖中的節點信息、節點存在與否動態變化，這要求模型泛化能力極強並且擁有很好的靈活性。
6. 有信息的邊：遇到帶信息的邊，需要考慮邊帶有的信息。現在有這麼幾個方法：（i）將邊變爲一個節點和兩條邊，這樣就去掉了信息邊。（ii）不同的邊擁有不同的參數矩陣（需要考慮參數數量問題）。

其github的地址：

GitHub - graphdeeplearning/benchmarking-gnns: Repository for benchmarking graph neural networks​ github.com