論文地址:https://arxiv.org/pdf/1908.01580v1.pdf
並行計算各層梯度並更新參數
解決梯度消失/爆炸問題
降低內存佔用
這就是代替反向傳播的 HSIC Bottleneck,反向傳播傳遞的梯度它也能計算,反向傳播帶來的各種缺點它也能彌補。
在這篇論文中,研究者介紹了用於訓練深度神經網絡的希爾伯特·施密特獨立準則(Hilbert-Schmidt independence criterion,HSIC)Bottleneck,用它來代替反向傳播簡直非常美妙了。
研究者表示,HSIC-Bottleneck 的表現在 MNIST/FashionMNIST/CIFAR10 分類中的表現與具有交叉熵目標函數的反向傳播算法相當。且只需要在訓練好的、已凍結參數 HSIC-Bottleneck 網絡上再增加一個基於 SGD 且沒有反向傳播一層網絡能夠實現圖像分類的 SOTA 性能。

標準反向傳播的可視化。
廣受讚譽的 HSIC-Bottleneck
雖然很多研究者都知道我們應該找一種比反向傳播更優秀的方法,但反向傳播應用太廣了,也非常直觀優美。因此,很難有研究者提出真正能 Work,且還非常有優勢的 BP 替代品。在這篇論文放到 Reddit 後,很多研究者都非常贊同這項工作,並表示這個領域非常值得關注。
DontShowYourBack 表示:「這篇論文的附加值並不在於它是否達到了 SOTA 結果,在我看來,作者設法使用了一種既不復雜、又不需要對稱反饋的機制,並獲得了很好的效果,這纔是真正重要的因素。理論上,它能應用於更低計算力的平臺和更獨特的架構,因爲這些是將反向傳播應用到當前硬件和架構上最大的挑戰。」
該用戶表明,他將親自研究這種方法,並希望能快速看到一些有趣的結果。
HSIC Bottleneck 的作者表示,反向傳播計算梯度的複雜度爲 O(D^3),其中 D 表示不同層級的神經元數量。因此整個神經網絡的反傳複雜度爲 O(LD^3),其中 L 表示層級數。但是對於 HSIC 來說,它的計算複雜度爲 O(M^2),其中 M 表示樣本數量,這樣整個網絡的計算複雜度爲 O(LM^2)。
值得注意的是,目前深度模型都是過參數化的,也就是說參數量要遠遠多於數據量,這樣計算量不就大大降低了嗎?
因此有用戶表明:「HSIC 最重要的部分就是將複雜度由反向傳播的 O(D^3) 降低到 O(M^2),這對於擁有數百萬或數十億參數量的神經網絡來說極其重要。」
HSIC 還有很多受到關注的屬性,目前機器學習社區也都在討論它。
探索 BP 替代品的這條不歸路
既然神經網絡可以視爲一個複雜的複合函數,且複合的次數就等於層級數,那麼將複合函數的求導法則「鏈式法則」作爲導數的獲取方式就非常直觀了。但最直觀的方法並不一定是最優的方法,反向傳播經常會因爲各種缺陷刺激着一批批研究者探索新的方法。
儘管反向傳播非常實用、優美,但它的速度、內存佔用、梯度消失/爆炸問題都困惑着一代代研究者。因爲前面層級的梯度必須等後面層級的梯度算完,BP 的速度比較慢;因爲 BP 需要保存前向傳播的激活值,所以顯存佔用比較高;因爲鏈式傳播的連乘方式,梯度非常容易爆炸或消失。
這些都是急需解決的問題,連提出 BP 的 Geoffrey Hinton 都對它充滿了質疑,在 17 年的 CapsNet 中,Hinton 老爺子嘗試通過 Dynamic Routing 找到更好的解,而且這種迭代並不需要反向傳播。Hinton 很早就意識到反向傳播並不是自然界生物大腦中存在的機制,也希望找到更好的反饋機制。

標準前傳與反傳的計算流程,其中紫色點表示計算結果需要保存在內存中。
針對傳播速度,DeepMind 之前曾提出了一種名爲解耦層的方法,它採用合成梯度近似經 BP 傳播的梯度,從而使前面層級與後面層級一同更新。而針對內存佔用,OpenAI 也曾嘗試做一個算力與內存間的權衡,他會以某種方式重算部分前傳結果,從而降低內存佔用。
但只要反傳還是鏈式法則,梯度消失和爆炸就不會真正得到解決。在這篇最新的論文中,研究者表示,如果我們直接最大會隱藏層與標註間的互信息,最小化隱藏層與輸入的相互依賴性,我們我們就能直接獲得對應的梯度,這種梯度是不需要反向傳播進行分配額的。因此模型在不要那麼多內存下快速更新權重參數,同時這樣也不會出現梯度爆炸或消失問題。
HSIC Bottleneck 到底是什麼
在論文中,研究人員說明,即使沒有反向傳播,模型依然可以學習分類任務,並獲得相當有競爭力的準確率。他們因此提出了一種深度學習網絡訓練方法。
這一方法由使用近似信息瓶頸的方法訓練而來。只要最大化隱層表示和標籤之間的互信息,並在同時最小化隱層表示和輸入的互相依賴關係即可。從信息瓶頸的角度來說,爲了減少模型依賴的參數量,所以要儘可能的讓隱層表示減少從輸入數據中獲得的信息量,而要儘可能讓隱層最大化地「榨乾」學習到的隱層表示,輸出正確的標籤預測結果。因此這一過程可以在儘可能減少數據依賴的情況下獲得能夠預測結果的信息。
由於計算互信息在隨機變量中較爲困難,研究人員選擇了基於非參數核的方法——希爾伯特·施密特獨立準則(HSIC),用來刻畫不同層之間的統計學依賴。換句話說,對於每個網絡層,研究人員都會同時最大化層和期望輸入之間的 HSIC,並最小化層和輸入之間的 HSIC。
研究人員進一步證明,按照這樣的訓練方式,網絡中的隱層單元可以組成很有用的表示。具體來說,凍結訓練好的 HSIC 網絡,在不需要反向傳播的情況下,僅更新和訓練一層單層的、使用了卷積 SGD 的網絡就可以達到很近似最佳準確率效果的模型
使用 HSIC-Bottleneck 的優勢在於,相比標準的反向傳播算法,網絡可以快速收斂。這是因爲 HSIC-Bottleneck 直接在連續隨機變量上進行運算,相比基於丟棄的傳統信息瓶頸方法更好。這一方法使用了一個傳統的弱訓練網絡用於將表示轉換爲輸出標籤的形式。在實際中,研究人員使用了一個網絡,包括很多層和多種維度(如果是全連接層),或者不同數量的核(如果是卷積層)作爲開始。
什麼是希爾伯特·施密特獨立準則
說起希爾伯特·施密特獨立準則,我們需要先談談信息瓶頸的問題。信息瓶頸描述的是最小需要多少數據能夠充分預測結果的理論,這是一個隱層表示上的權衡問題,即可以預測輸出所需的信息量和輸入中應當保留多少信息之間的權衡。信息瓶頸原則決定了需要保留多少關於標籤的隱層表示信息,而需要壓縮多少輸入中的信息。
根據信息瓶頸,我們就可以知道,在訓練機器學習模型時,需要對至少多少的輸入信息進行保留,以便隱層表示能夠預測出和標籤相符結果的數據量。
而要計算這個保留的信息量是非常困難的。此外,傳統的信息瓶頸理論大部分基於丟棄信息的方法,因此作者選擇了基於希爾伯特·施密特獨立準則的信息瓶頸方法,用於獲得機器學習過程中的梯度。
那麼,什麼是希爾伯特·施密特獨立準則呢?理論上,希爾伯特·施密特獨立準則可以發現變量之間的任意依賴。當給定正確的核大小(如高斯核)的時候,HSIC 當且僅當兩個隨機變量完全獨立時爲 0。因此,只要是兩個變量之間具有非獨立的關係,HSIC 就可以以非參數化的方式將其刻畫出來。
用 HSIC 訓練的網絡是什麼樣的
使用 HSIC-Bottleneck 目標訓練深度學習的網絡被稱爲 HSIC-Bottleneck 訓練或預訓練。Bottleneck 訓練網絡的輸出包括分類的必要信息,但不是正確的形式。
研究人員評價了兩種從 HSIC 評價訓練網絡產生分類結果的方法。首先,如果輸出是獨熱向量,則可以根據訓練標籤被直接重新排列。在第二個場景下,研究人員將一個單層和 softmax 輸出層連接到了凍結的 Bottleneck 訓練網絡後,並使用沒有反向傳播的 SGD 方法訓練這個額外增加的層。這一步驟被稱爲後訓練(post-training)。

圖 1:HSIC 訓練的網絡(1a)。這是一個標準的前向傳播網絡,但是使用了 HSIC IB 目標函數,這樣可以使最後一層的隱層表示快速地開始訓練。圖 1b 則展示了一個名爲「σ-組合」的網絡,每個網絡分支都有一個特定的σ進行訓練。因此,對於從 HSIC 網絡中訓練的每個隱層表示都可能包含在特定尺度下從 HSIC-Bottleneck 目標函數中獲得的不同信息。之後,聚合器會將隱層表示相加,組成一個輸出表示。
研究人員展示的 HSIC 訓練網絡是如下的一個前向輸入網絡。
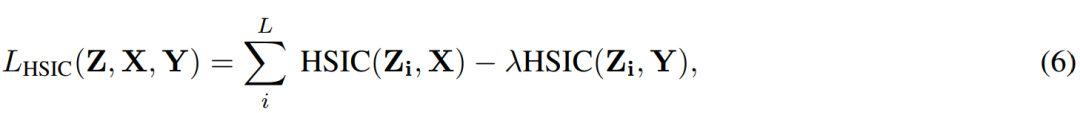
在網路中,Z = {Zi}, i ∈ {0, ..., L},L 則是隱層的數量。HSIC 訓練網絡可以被理解爲是優化的編碼 PθT (Zi |X) 層和 PθT (Y |Zi) where i ∈ {0, ..., L} 解碼層。這個網絡提供了包含用於分類任務信息的隱層。
HSIC-trained 神經網絡效果怎麼樣
首先,研究者繪製了 HSIC-bottleneck 值與激活值的分佈,它們都是在訓練中從簡單的模型採樣得出。其次,研究者還提供了 HSIC-bottleneck 和標準反向傳播之間的對比,它們都在相同數據集上使用相同參數量的前饋網絡測試得出。
在對比實驗中,研究者在 MNIST/Fashion MNIST/CIFAR-10 數據集上訓練前饋網絡,並分析了 HSIC-bottleneck 在處理經典分類任務上的表現。其中,前饋網絡還包括非常著名的 ResNet。在研究者完成的所有實驗中,都包含了標準反向傳播、預訓練和後訓練階段,後訓練階段使用的都是 SGD 最優化器。
HSIC-bottleneck 的值長什麼樣
圖 2 展示了 HSIC-bottleneck 的值在訓練深度網絡時的變化。
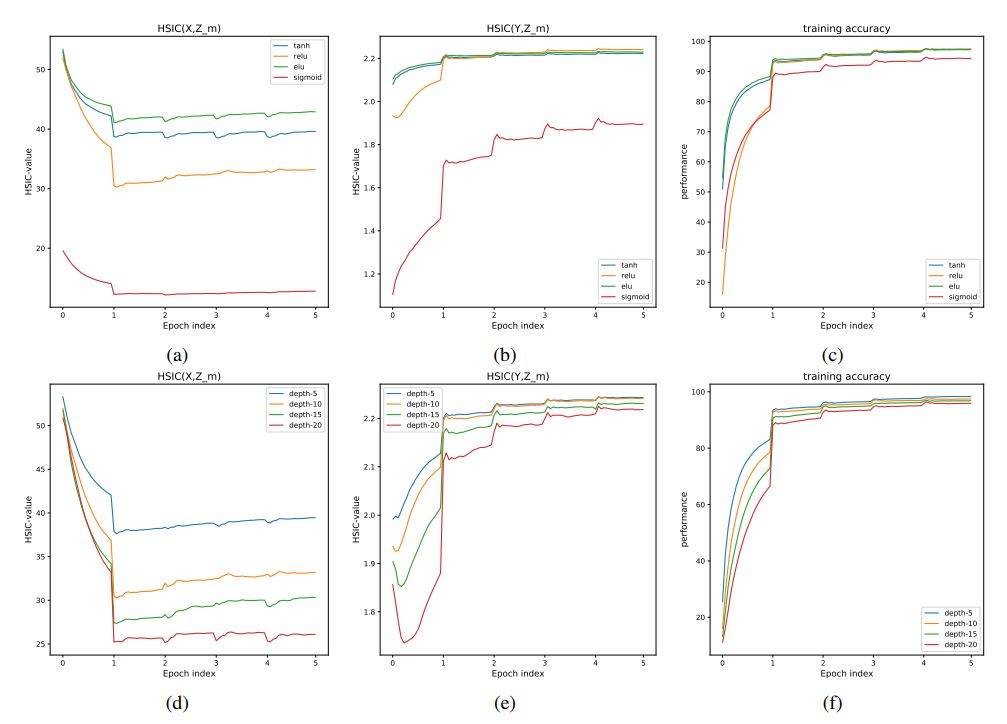
圖 2:這些實驗展示了,在傳統反向傳播訓練過程中,隨着網絡激活函數 (2a)-(2c) 和深度 (2d)-(2f) 的變化,HSIC-bottleneck 數量 HSIC(X, ZL) 和 HSIC(Y, ZL) 的變化,以及訓練準確率的變化。
圖 3a 和 3b 可視化了前饋網絡中最後一個隱藏層每一個類別的激活值。
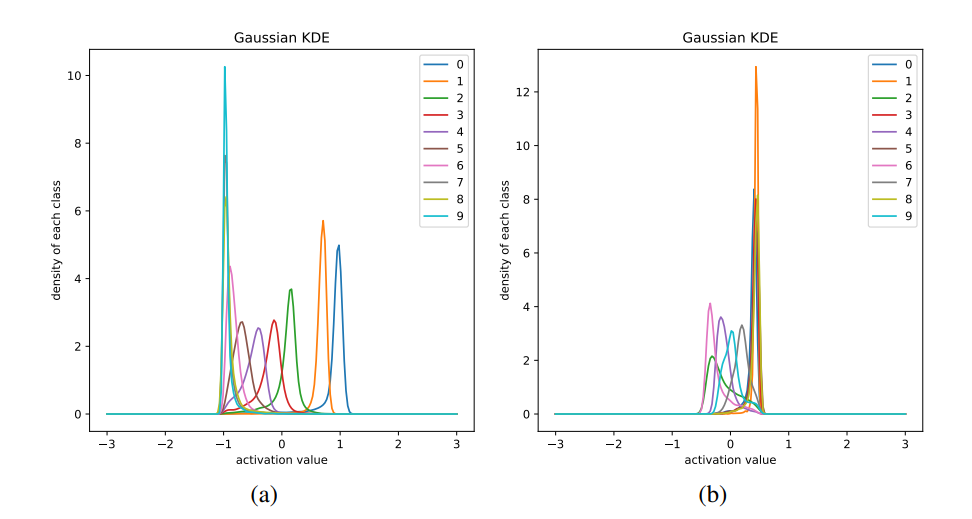
圖 3:最優一層 tanh 激活函數值的分佈,其神經網絡各層的隱藏單元數爲:784-64-32-16-8-4-2-1,它通過 HSIC-bottleneck 目標 (3a) 和反向傳播 (3b) 訓練。

圖 4:MNIST 輸出類別的分佈,每一張子圖都展示了類別及對應的分類準確率。
HSIC-bottleneck 效果怎麼樣
圖 5 展示了反向傳播和論文提出的 HSIC 評價訓練方法。在第一個訓練輪中,論文提出的方法的表現就超過了標準的機器學習訓練方法,分別在 Cifar 10,FashionMNIST 和 MNIST 上取得了 43%、85% 和 95% 的效果。在訓練結束後,HSIC-Bottleneck 訓練的網絡表現和其他標準反向傳播算法幾乎一致。

圖 5:論文提出的 HSIC 評價訓練方法在標準的分類問題上的表現。實驗使用了同樣的訓練配置,但是批大小不同。傳統反向傳播使用了 32 和 256 的批大小,但 HSIC 算法只使用了 256 的批大小。
在圖 8 中,研究人員展示了一個有着 5 個卷積殘差塊的 HSIC 訓練的網絡在不同數據集上的表現。每個實驗都包括了 50 個 HSIC 訓練輪,之後每個網絡都會進行後訓練——用一個單層分類網絡進行,這和標準反向傳播訓練網絡不同。

圖 8:在不同數據集上 ResNet 後訓練的效果。
相關鏈接:https://arxiv.org/abs/1908.01580v1
https://www.reddit.com/r/MachineLearning/comments/cql2yr/deep_learning_without_backpropagation/