瑞利-貝納德對流（Rayleigh–Bénard Convection）。利用有限元方法將空間上連續的問題離散化，將複雜的關係歸納偏差顯示爲實體集合。資料來源：原作者。
多智能體系統被廣泛應用於各種不同的科學領域：從物理學到機器人學、博弈論、金融學和分子生物學等等。通常來說，預測或決策任務依賴於具有噪聲且無規則採樣的的觀測，因此封閉形式的分析公式對此是無效的。
這類系統對關係歸納偏差提供了生動形象的樣例。在樣本統計或機器學習過程中引入歸納誤差，是一種普遍用於提高樣本有效性和泛化性的方式。從目標函數的選擇到適合某項具體問題的自組織深度學習的框架設計，設定偏差也是非常常見且有效的方式。
關係歸納偏差[1]代表一類特殊的偏差，涉及實體之間的關係。無論是圖形模型、概率模型還是其他模型，都是一類專門對實體施加先驗結構形式的關係偏差的傳統模型。這些圖形結構能夠在不同領域中發揮作用，它可以通過引入條件獨立性假設來降低計算複雜度，也可以通過將先驗知識編碼爲圖的形式來增強樣本的有效性。
圖神經網絡（GNN）是圖模型對應的深度學習網絡。GNN 通常會在這兩種情況中使用：一是當目標問題結構可以編碼爲圖的形式；二是輸入實體間關係的先驗知識本身可以被描述爲一張圖。
GNN 在許多應用領域都展示了顯著的效果，例如：節點分類[2]、圖分類、預測[3][4]以及生成任務[5]。
一、深度學習中的常微分方程
一種類型不同但重要性相等的歸納偏差與收集到數據所使用系統的類別相關。儘管從傳統上看，深度學習一直由離散模型主導，但在最近的研究提出了一種將神經網絡視爲具有連續層的模型[6]的處理方法。
這一觀點將前向傳播過程，重定義爲常微分方程（ODE）中初值求解的問題。在這個假設下，可以直接對常微分方程進行建模，並可以提高神經網絡在涉及連續時間序列任務上的性能。
《Graph Neural Ordinary Differential Equations》這項工作旨在縮小几何深度學習和連續模型之間的差距。圖神經常微分方程（Graph Neural Ordinary Differential Equations ，GDE）將圖結構數據上的一般性任務映射到一個系統理論框架中。我們將常見的圖結構數據放入系統理論框架中，比如將數據結構化到系統中：
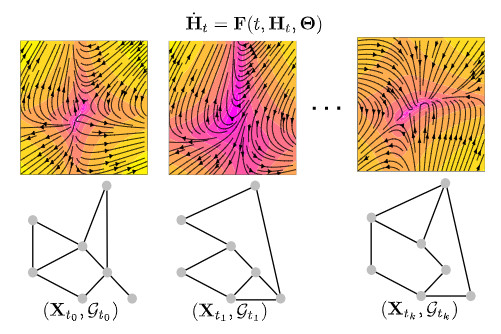
無論 GDE 模型的結構是固定還是隨時間變化的，它都可以通過爲模型配備連續的 GNN 圖層來對定義在圖上的向量場建模。
GDE 模型由於結構由連續的 GNN 層定義，具備良好的靈活性，可以適應不規則序列樣本數據。
GDE 模型的主要目的是，提供一種數據驅動的方法爲結構化系統建模，特別是當這個動態過程是非線性時，更是難以用經典的分析方法進行建模。
下面是對GDE的介紹。關於更多細節和推導，請參閱原論文，論文相關鏈接如下：
目前我們正在開發一個用於介紹GDE模型的 Github Repository（倉庫），其中包含使用 Jupyter notebook 且帶有註釋的相關示例，Github 相關地址如下：
據悉，我們正計劃將它最終部署成具有不同功能的設置（包括預測、控制…），其中包括所有主要圖形神經網絡（GNN）架構下不同 GDE 變體的工作示例。
二、序言和背景
GDE 和 GNN 一樣，都是在圖上進行操作。關於符號和基本定義更詳細的介紹，我們參閱了關於 GNN 的優秀的相關綜合研究（相關研究鏈接爲：https://arxiv.org/abs/1901.00596）以及原論文中的背景部分。
下面，我們將對 GDE 進行簡要的介紹，不夠實際上，只有下面兩點關於圖的基本知識是我們即將需要了解到的：
1、圖是由邊連接的互連節點（實體）的集合。深度學習模型通常處理用一組特徵（通常以一組向量或張量）描述節點的屬性圖。對於 n 個節點的圖，每個節點都可以用 d 個特徵描述，最後我們將這 n x d 個節點嵌入矩陣表示爲 H。
2、圖的結構由其鄰接矩陣 A 捕獲。節點之間的連通結構表現出標準深度學習模型和GNN模型之間的主要區別[1]，因爲GNN直接以各種方式利用它對節點嵌入進行操作。
三、圖神經常微分方程
圖神經常微分方程（GDE）定義如下：
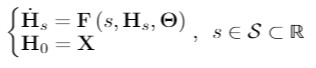
GDE的一般公式
其中，H是節點特徵矩陣。上式中定義了函數 F 參數化的 H 的向量場，其中函數 F 可以是任意已知的圖神經網絡（GNN）層。
換句話說，F 利用圖 G 節點的連接信息及其節點特徵來描述 H 在 S 中的變化過程。其中，S 是模型的深度域；不同於 GNN 由自然數的子集來指定的深度域，S 是連續的，它表示由函數 F 定義的常微分方程的積分域。
GDE 可以通過多種方式進行訓練，這一點很像標準的神經常微分方程[6]。原論文中也對系統的適定性進行了詳細闡釋和討論。
一般的 GDE 公式帶有幾種含義。在一般神經常微分方程中，觀察到選擇離散化方案可以對 ResNets（殘差網絡）已知的先前離散多步驟變量進行描述[7]。因此，深度學習中連續動態系統的觀點不僅侷限於微分方程的建模，而且可以利用豐富的數值方法相關文獻來指導發現新的通用模型。
與 ResNets 相比，GNN 作爲一個模型類別來說算是相對年輕的。因此，關於多步驟的複雜變體以及類似分形殘差連接的相關文獻發展得並沒有那麼完善；而我們可以發現一些新的 GNN 變體是通過應用GDE的各種離散化方案來指導的，而不是完全從頭開始。
靜態圖結果：節點分類
通過在 Cora、Pubmed 和 Citeseer 上進行一系列半監督節點分類實驗，證明 GDE 可以作爲高性能的通用模型。這些數據集包含靜態圖，其中鄰接矩陣 A 保持不變，從而使其遠離運用GDE的動態系統設置。我們評估圖卷積常微分方程（GCDE）的性能，定義爲：
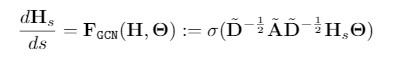
GCDE模型。在我們的論文中包含了一個更加詳細的版本，以及一些GNN流行的GDE變體版本。
它們的完全離散的形式對應圖卷積網絡（GCN）[8]。我們參考了包括著名的圖注意力網絡（GAT）[9]在內的文獻作爲參考：
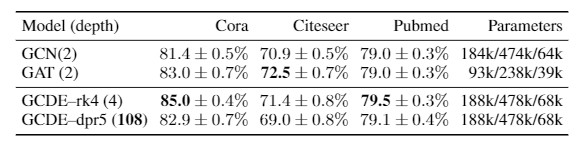
節點分類任務的準確性。上表取值爲100次運行的平均值和標準偏差。
GCDE 被證明可以媲美最先進的模型，並且優於它們的離散模型。我們評估瞭如下兩種 GCDE的版本：
一種是離散的固定步長的方案，採用 Runge-Kutta4（GCDE-rk4）；
另一種是自適應步長方案，採用 Dormand-Prince（GDDE-dpr5）。
固定步長的離散方案並不能保證 ODE 近似仍然接近解析解；在這種情況下，求解一個適當的 ODE 是不必要的，GCDE—rk4能夠提供一個計算效率高的類子結構的FractalNet（比如GCN模型的結構）來提高準確率。
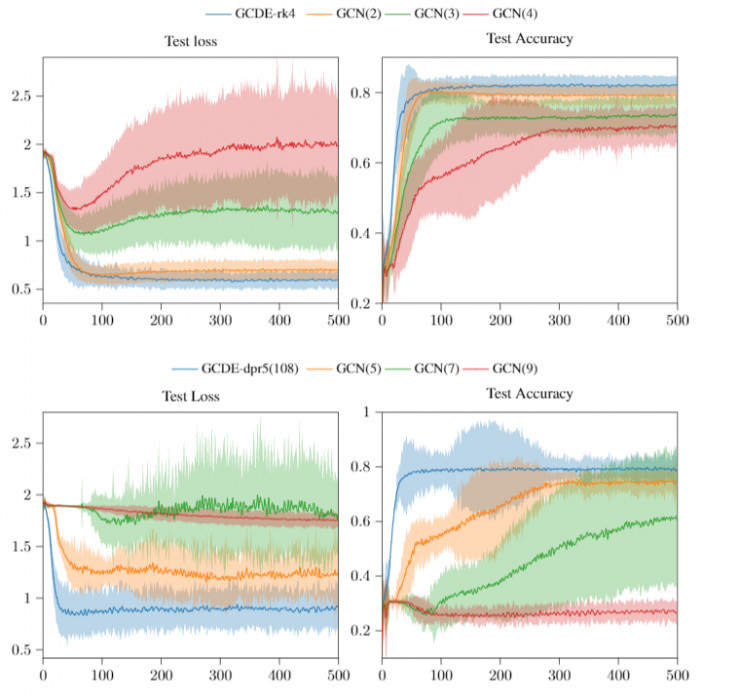
如圖爲Cora的訓練損失和準確率，其中陰影區域是95%置信區間
另一方面，使用自適應步長解算器訓練 GCDE 自然會比使用 vanilla GCN 模型的深度更深，後者網絡層的深度使該網絡性能大大降低。
實驗中我們成功地訓練了GCDE-dpr5，它有多達200個ODE函數評估（NFE），這使得它對圖中的計算量明顯高於vanilla GCN（由於層數太深使得性能大幅度降低）。應該注意的是，由於GDE在求解函數中會對參數重利用，它比對應的離散項需要更少的參數。
有趣的是，自適應步長GDE似乎不受節點特徵過度平滑的影響。過度平滑問題[10]阻礙了深層GNN在各個領域的有效使用，特別是在多智能體強化學習（MARL）中，我們目前正在積極探索GDE這一特性，並能夠很快進行更爲詳細的分析。
四、時空 GDE
GDE 中一項關鍵的設定涉及到時空圖數據信息。在處理圖的序列信息時，需要用到 GNN 的遞歸版本 [11][12]。
然而， 與常規的遞歸神經網絡（RNN）及其變體一樣，在固定的離散度的情況下不允許其對不規則的樣本數據進行操作。這一事實進一步推動了基於到達次數之間的變動的先驗假設下 RNN 形式的發展，比如 RNN 的 ODE 版本 [14] 。
在涉及時間分量的場景中，GDE 中 S 的深度域與時間域一致，並且可以根據需求進行調整。例如，給定時間窗口 Δt，使用 GDE 進行預測的公式形式如下：
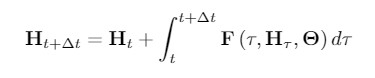
儘管擁有特殊的結構，GDE 代表了一類圖序列的自迴歸模型，以混合動態系統的形式自然地通往擴展的經典時空結構，比如：以時間連續和時間離散的動力學相互作用爲特徵的系統。
它的核心思想是，讓一個 GDE 在兩種時間點之間平滑地控制潛在的節點特徵，然後應用一些離散算子，讓節點特徵 H 快速移動，接着由輸出層來處理這些節點特徵 H 。
給定一系列的時間常數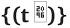
以及一種數據的狀態——圖數據信息流
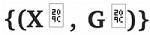，自迴歸 GDE 的一般公式爲：
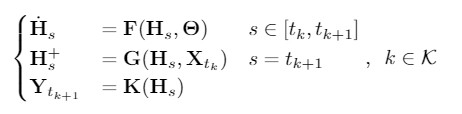
如圖爲自迴歸GDE。擁有已知連續變量的時空GNN模型可以通過從這個系統中通過選擇合適的F，G，K參數來獲得。
其中，參數 F，G，K 是類似於 GNN 的操作或者一般的神經網絡層，H+表示經過離散變換後的 H 值。該系統的轉變過程可以通過混合自動機進行可視化處理：
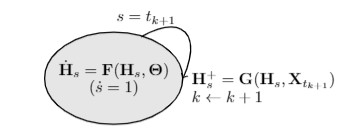
自迴歸 GDE的混合自動機原理圖
與只具有離散跳躍的標準遞歸模型相比，自迴歸 GDE 在跳躍間包含了一個潛在特徵節點的連續流 H。自迴歸 GDE 的這一特性使它們能夠從不規則的觀測結果中來跟蹤動態系統。
F，G，K 的不同組合可以產生最常見的時空 GNN 模型的連續變量。
爲了評估自迴歸 GDE 模型對預測任務的有效性，我們在建立的 PeMS 流量數據集上進行了一系列實驗。我們遵循文獻[15]的實驗預設參數，並且附加了一個預處理步驟：對時間序列進行欠採樣，爲了模擬在具有不規則時間戳或有缺失值等具有挑戰性的環境，這裏將每個輸入以 0.7 的概率進行刪除。
爲了在由連續時間系統生成的數據設置中測量 GDE 獲得的性能提升，我們使用 GCDE-GRU 及其對應的離散 GCGRU[12]，並將結果置於 vanilla GRU 度量標準中進行測量。
對於所考慮的每個模型，我們收集了標準化 RMSE（NRMSE）和平均絕對百分比誤差（MAPE）結果。關於所選指標和數據的更多細節請參見原論文。
由於在訓練和測試過程中平均的預測時間範圍會發生急劇變化，這種時間戳之間的非恆定差異導致單個模型的預測任務更加具有挑戰性。爲更加公平的對模型進行比較，我們將增量時間戳信息作爲 GCGN 和 GRU 的附加節點特徵。
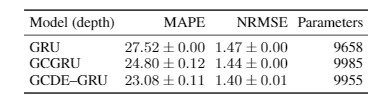
不規則數據預測任務的結果。此處取5次訓練的平均值和標準差。
由於 GCDE-GRU 和 GCGRU 的設計在結構和參數數量上是匹配的，我們可以在 NRSME 中測量到 3% 的性能增長，在MAPE中測量到7%的性能增長。
對具有連續動態和不規則數據集的其他應用領域採用 GDE 作爲建模工具，也將同樣使其擁有優勢，例如在醫學、金融或分佈式控制系統等領域。我們正在這些領域進行另外的一些相關實驗，歡迎提出任何要求、想法或合作意見。
六、結論
如上所述，我們目前正在開發一個Github庫，其中包含一系列針對 GDE 模型不同類型的示例和應用程序。
我們鼓勵大家對GDE的其他應用程序在Github中進行請求/建議操作：我們計劃它最終可以包括所有主流圖神經網絡（GNN）架構的GDE變體的相關工作示例，部署在各種設置（預測、控制…）之中。
我們的論文可以在arXiv上作爲預印本：如果您覺得我們的工作有用，請考慮引用我們的論文。
參考文獻
[1] P. W. Battaglia et al. Relational inductive biases, deep learning, and graph networks. arXiv preprint arXiv:1806.01261, 2018.
[2] J. Atwood and D. Towsley. Diffusion-convolutional neural networks. In Advances in Neural Information Processing Systems, pages 1993–2001, 2016.
[3] Z. Cui, K. Henrickson, R. Ke, and Y. Wang. Traffic graph convolutional recurrent neural network: A deep learning framework for network-scale traffic learning and forecasting. arXiv preprint arXiv:1802.07007, 2018
[4] J. Park and J. Park. Physics-induced graph neural network: An application to wind-farm power estimation.Energy, 187:115883, 2019.
[5] Li, O. Vinyals, C. Dyer, R. Pascanu, and P. Battaglia. Learning deep generative models of graphs. arXiv preprint arXiv:1803.03324, 2018.
[6] T. Q. Chen, Y. Rubanova, J. Bettencourt, and D. K. Duvenaud. Neural ordinary differential equations. In Advances in neural information processing systems, pages 6571–6583, 2018.
[7] Y. Lu, A. Zhong, Q. Li, and B. Dong. Beyond finite layer neural networks: Bridging deep architectures and numerical differential equations. arXiv preprint arXiv:1710.10121, 2017.
[8] T. N. Kipf and M. Welling. Semi-supervised classification with graph convolutional networks. arXiv preprint arXiv:1609.02907, 2016.
[9] P. Velickovic, G. Cucurull, A. Casanova, A. Romero, P. Lio, and Y. Bengio. Graph attention networks. arXiv preprint arXiv:1710.10903, 2017.
[10] Chen, Deli, et al. 「Measuring and Relieving the Over-smoothing Problem for Graph Neural Networks from the Topological View.」 arXiv preprint arXiv:1909.03211 (2019).
[11] Y. Li, R. Yu, C. Shahabi, and Y. Liu. Diffusion convolutional recurrent neural network: Data-driven traffic forecasting. arXiv preprint arXiv:1707.01926, 2017
[12] X. Zhao, F. Chen, and J.-H. Cho. Deep learning for predicting dynamic uncertain opinions in network data. In 2018 IEEE International Conference on Big Data (Big Data), pages 1150–1155. IEEE, 2018.
[13] Z. Che, S. Purushotham, K. Cho, D. Sontag, and Y. Liu. Recurrent neural networks for multi-variate time series with missing values.Scientific reports, 8(1):6085, 2018.
[14] Rubanova, R. T. Chen, and D. Duvenaud. Latent odes for irregularly-sampled time series. arXiv preprint arXiv:1907.03907, 2019.
[15] B. Yu, H. Yin, and Z. Zhu. Spatio-temporal graph convolutional networks: A deep learning framework for traffic forecasting. In Proceedings of the 27th International Joint Conference on Artificial Intelligence (IJCAI), 2018.
via https://towardsdatascience.com/graph-neural-ordinary-differential-equations-a5e44ac2b6ec