【斯坦福CS224W 圖與機器學習(P1-P2)】：圖模型基本介紹

2020-05-05 20:25:35.0

圖網絡最近幾年越來越火啦！推薦斯坦福CS224W這門課，適合初學者入門，也適合有一定基礎的同學進行一個梳理~

課程鏈接：（裏面包括了ppt，課後補充閱讀材料）

CS224W | Home web.stanford.edu

b站鏈接：（視頻有中文字幕，雖然翻譯的有點==，還是可以幫助理解的！）

【斯坦福】CS224W：圖機器學習2019秋（ GNN | 中英字幕）_嗶哩嗶哩 (゜-゜)つロ乾杯~-bilibili www.bilibili.com

課程一共21節，21天打卡，簡單記錄下每節課的筆記~

Graph Types

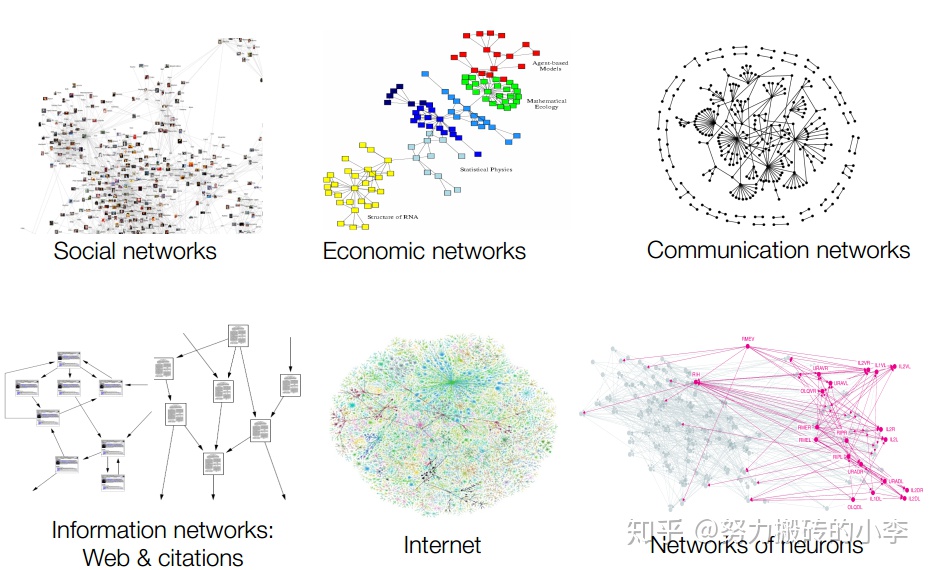
圖在生活中無處不見，有天然的圖網絡，也有人爲構造的網絡：

Natural Graphs

社交網絡：比如Facebook，Twitter，微博
基因/蛋白至連接的網絡
大腦中神經元的連接

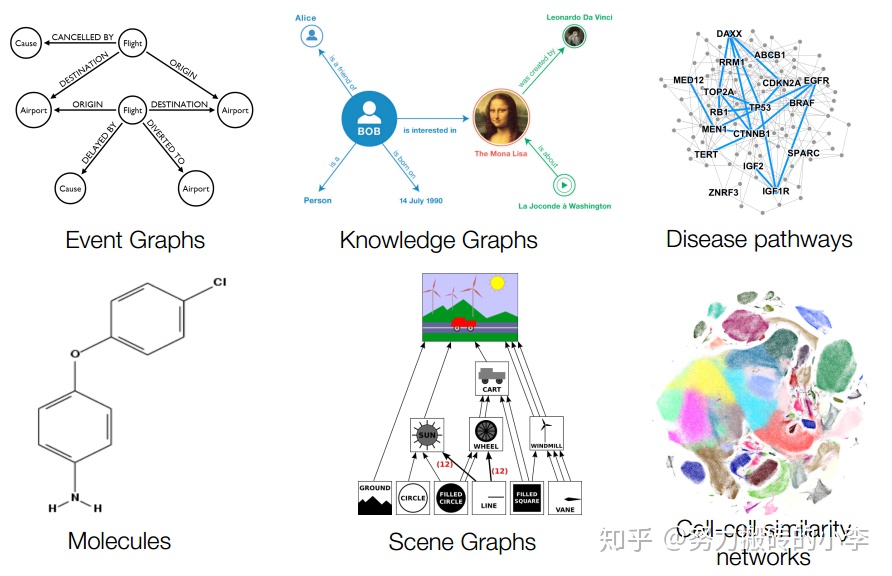
Information Graphs

(我的理解就是非天然網絡，根據交互關係人爲構造的網絡）

信息/知識圖：比如說引文網絡，如果一篇文章引用了另外一篇文章，則這兩篇文章有一條邊相連；
場景圖：捕捉場景中目標的交互，比如說在電子商務中，A用戶瀏覽了B商品，則有一條邊相連（這類圖就可以用於推薦問題）
相似性網絡：如果用戶AB的相似度大於某一閾值，則有一條邊相連

圖網絡分析方法

節點分類：判斷節點的類型，比如說在異常檢測問題中區分正常用戶與異常用戶
鏈接預測：兩個節點是否有邊相連，比如說推薦網絡中預測用戶A是否會購買商品B；也可以判斷兩個節點的社交關係(朋友，家人等)
社區發現：網絡中的社交圈的檢測，比如說劃分出一個網絡中家庭成員、朋友、大學同學、高中同學的社交圈，可以理解爲一種聚類方法
相似度度量：衡量兩個節點的相似度，比如說可以通過學習到每個節點的低維向量表示後，衡量節點之間的相似度。

圖的基本結構

一個圖可用 $G(V,E)$ 表示，其中 $V$ 爲節點， $E$ 爲邊，一個圖最關鍵的信息就是節點是什麼？邊是什麼？

圖的類型

無向圖：Facebook中好友關係圖
有向圖：微博關注粉絲圖
完全圖：所有節點之間都有邊相連
無權圖：圖的節點之間沒有權重
加權圖：圖的節點之間有權重
自環圖：有邊指向節點自己
多重圖：兩個節點之間有多個邊
二分圖：節點可以被分爲兩類U和V，每一條邊對應的兩個節點都分別來自U和V，即集合U和V內部沒有邊。比如說作者-論文圖、演員-電影圖、用戶-電影評分圖，這類圖可以被「摺疊」爲正常網絡，比如說在作者-論文圖中，如果兩個作者同時出現在一篇論文中，則有一條邊相連，這樣摺疊後的節點只有作者這一類。
連通圖：任意兩個節點之間都可以找到一條路徑

圖網絡性質

度分佈 $P(k)$
路徑長度 $h$
聚類係數 $C$
連通分支 $s$

簡單說下這幾個性質：

度分佈：衡量每個節點的度的分佈情況
路徑長度：

直徑：圖中任意兩點的最短路徑的最大值

平均路徑長度： $\bar{h}=\frac{1}{n(n-1)}\sum_{i,j\neq i}h_{ij}$ ，其中 $h_{ij}$ 爲節點i到節點j的距離， $n(n-1)$ 爲考慮有向圖時圖中最大邊數（無向圖邊數×2），通常只在連通圖中考慮平均路徑長度，即忽略路徑爲無窮的邊。

聚類係數： $C_i = \frac{2e_i}{k_i(k_i-1)}$ ，其中 $e_i$ 是節點i鄰居節點之間相連的邊個數， $k_i$ 是節點i的度數，在下圖中，計算每個圖節點i的聚類係數：左圖中 $C_i=\frac{2*6}{4*3}=1$ ，中間的圖中 $C_i=\frac{2*3}{4*3}=\frac{1}{2}$ ，右圖中 $C_i=\frac{2*0}{4*3}=0$ ，聚類係數可以看作衡量鄰居的聚集情況，像左圖中，鄰居聯繫密切，而右圖中，鄰居之間沒有任何連接。整個圖的聚類係數爲每個節點的平均聚類係數： $C=\frac{1}{N}\sum_i^NC_i$

連通分支：圖中連通的最大集合

真實網絡 & 隨機網絡

對於不同的圖網絡，比較上述四個性質，真實網絡利用了MSN，先介紹一下隨機網絡。

兩種定義方式：

$G_{np}$ ：無向圖有n個節點，每條邊 $(u,v)$ 以概率p相連
$G_{nm}$ ：無向圖有n個節點，隨機選取m條邊相連

對 $G_{np}$ 分析上述四個性質：

度分佈：滿足二項分佈 $P(k)=C_{n-1}^kp^k(1-p)^{n-1-k}$ ，也很好理解，對於除當前節點之外的n-1個節點中隨機選取k個，每條邊都是以概率p連接。則度分佈的均值爲： $\bar{k}=p(n-1)$ ，方差爲 $\sigma^2=p(1-p)(n-1)$ ，則 $\frac{\sigma}{\bar{k}}=\sqrt{\frac{1-p}{p}\frac{1}{n-1}}\approx \frac{1}{(n-1)^{1/2}}$ ，可以看出當n足夠大，樣本足夠多的時候，每個節點的度近似是相同的
路徑長度：可以理解爲BFS遍歷圖，對於連通圖來說，每次訪問的是當前節點的鄰居，對於隨機圖來說，這棵樹的深度爲 $log_{np}n=\frac{log \ n}{log \ np}$
聚類係數：由於 $C_i=\frac{2e_i}{k_i(k_i-1)}$ ，其中 $e_i$ 是節點i鄰居節點之間相連的邊數，

對於度數爲 $k_i$ 的節點，鄰居節點對數爲 $\frac{k_i(k_i-1)}{2}$ ，每對節點以概率p相連，

則 $E(e_i)=p\frac{k_i(k_i-1)}{2}$ ，

$E(C_i)=\frac{pk_i(k_i-1)}{k_i(k_i-1)}=p=\frac{\bar{k}}{n-1}\approx\frac{\bar{k}}{n}$

可以看出，當n足夠大，樣本足夠多時，聚類係數接近於0，即鄰居之間沒有連接。

連通分支：圖的結構隨着p的變化而改動，如下圖所示，當p爲0時，爲空圖，即沒有邊相連，當p爲1時，爲完全圖，即任意兩個節點之間均有邊相連，當p=1/(n-1)時，由於度數的均值爲 $p(n-1)=1$ ，即此時爲連通圖。

現在，對比一下真實網絡圖MSN與隨機圖 $G_{np}$ ：

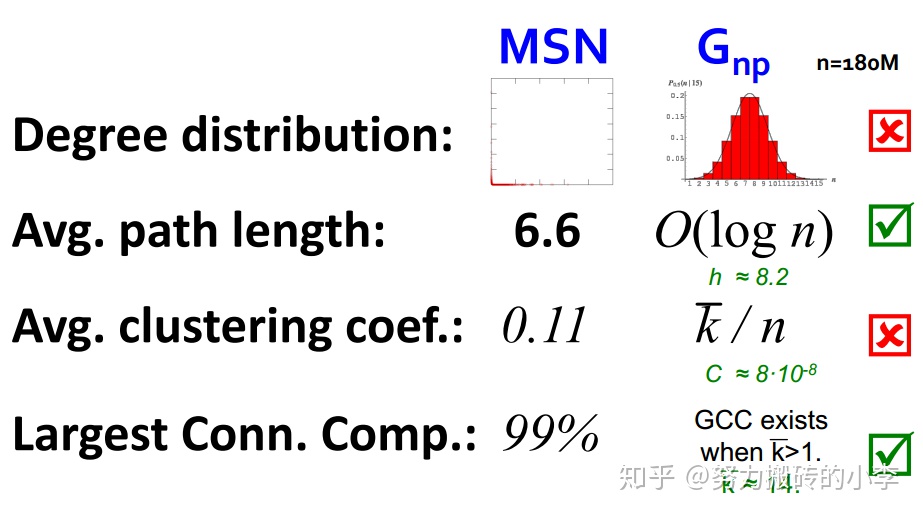
可以看出，對於平均路徑長度和連通分支來說，二者近似相同，而度分佈和平均聚類係數來說，二者相差較大。所以隨機網絡並不可以模擬真實世界中的網絡

The Small-World Model 小世界模型

由上述分析可知，隨機網絡較好的模擬了真實數據中平均路徑長度，但是卻遠遠低估了聚類係數。在真實網絡中，聚類係數應該是比較高的（比如說，朋友的朋友大概率也是我的朋友），因此希望可以有一種模型，在平均路徑較小的條件下，聚類係數較高，就有了小世界模型。

小世界模型構造

首先產生一個標準的網絡，有較高的聚類係數，和較大的直徑，如下圖左所示
按照一定概率，將一條邊的另一個端點連接到任意較遠的節點上，如下圖中間所示，這樣仍然可以保持高聚類係數，但是圖的直徑減小了，即生成了小世界網絡

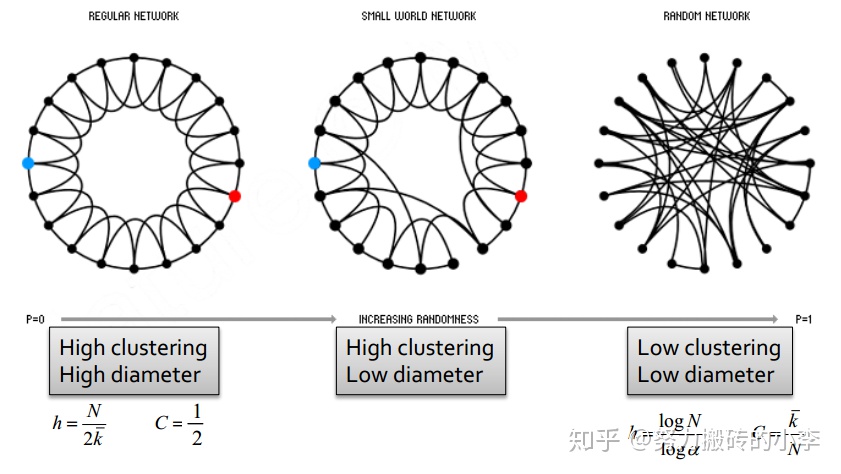
上圖所示，左邊爲標準網絡，中間爲小世界網絡，右邊爲隨機網絡，小世界網絡可以有較高的聚類係數，較小的直徑，但是小世界網絡的度分佈可能會有一定的偏差。

Kronecker Graph Model

可以利用Kronecker網絡模擬真實網絡，它的想法就是自相似度，就是利用Kronecker內積自己對自己迭代。

Kronecker內積：對於 $A\otimes B$ 如果A是一個m*n的矩陣，B是一個p*qn的矩陣，則結果爲一個mp*nq的矩陣：

更具體的：

舉例來說：

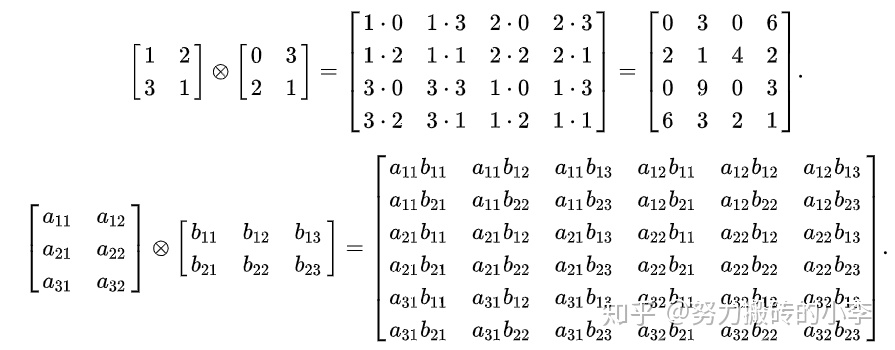
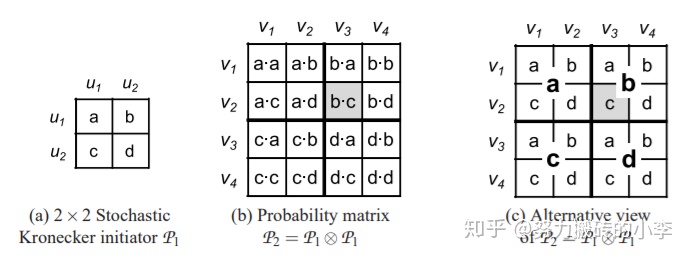
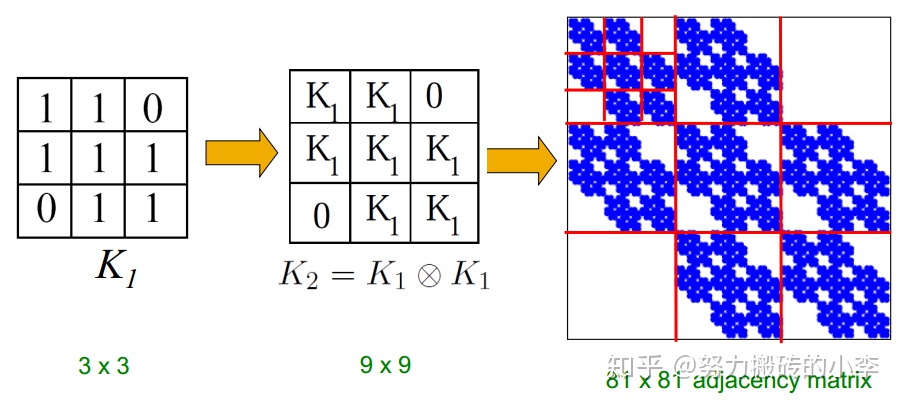
則在Kronecker圖中，可以利用類似的方法生成圖，如下圖所示， $K_1$ 爲初始的鄰接矩陣，經過兩次的Kronecker乘積得到 $K_3$ 爲81維的鄰接矩陣。

可以引入隨機性，即初始時不利用鄰接矩陣，而是概率矩陣，如下圖所示，矩陣中每個元素表示該位置有邊的概率，依據最終的這個概率矩陣就可以得到最終的圖。

另外，想要快速產生Kronecker圖，可以利用分解方法，如下圖所示，在生成的圖 $P_k$ 中每個節點 $v_i$ 可用一個序列 $(v_i(1),...v_i(k))$ 表示，其中 $v_i(l)\in \{u_1, ..., u_k\}$ ，則對於節點i和j有邊 $(v_i,v_j)$ 的概率爲： $p(v_i,v_j)=P_k[v_i, v_j]=\prod_{l=1}^kP_l[v_i(l),v_j(l)]$ 。關於Kronecker Graphs，可以參考論文：Kronecker Graphs:An Approach to Modeling Networks

文章來源：知乎