訓練一個深度神經網絡以實現最佳的性能是一件具有挑戰的任務。在本文中,我將會探索這項任務中最常見的問題及其解決方案。這些問題包括網絡訓練時間過長,梯度消失與爆炸以及網絡初始化,我們在此統稱爲優化問題。而在訓練網絡中出現的另一類問題則稱作正則化問題,對此,我已經在之前的文章中討論過了,如果你沒有閱讀過,可以點擊下方鏈接閱讀原文。
Improving Deep Neural Networks
輸入數據標準化
當我們在訓練神經網絡時,我們可能會注意到模型訓練的時間比預期的要久。這是因爲網絡的輸入數據沒有進行標準化處理,讓我們嘗試通過下方兩個輸入特徵來理解標準化的含義。
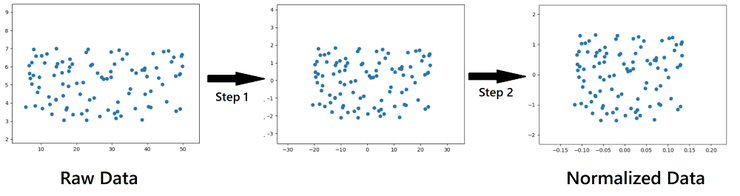
在原始數據中,數據的 X 軸(特徵X)取值區間爲5-50,Y軸(特徵Y)取值區間爲3-7。 另一方面,在標準化後的數據中,X軸取值區間時-0.15~0.15, Y軸的取值區間時-1.5~1.5。
通過標準化數據,即縮放數值從而使其特徵範圍非常接近:而標準化數據只需要兩步過程。
讓數據減去其均值,使得數據的均值爲 0,之後再讓該數據除以其方差,從而縮放數據。
mu = np.mean(X)
X = X - mu
sigma = np.linalg.norm(X)
X = X/sigma
這裏有一點值得注意的是,我們需要使用同樣的 mu 值和 sigma 值去轉換我們的測試數據,因爲我們想用同樣的方法來縮放它們。
爲什麼標準化會起作用呢?
既然我們已經知道了如何標準化數據集,那麼讓我們試着理解爲什麼標準化能夠在下面的示例中起作用。下面是成本值 J,權重 W 和偏差 b 之間的等高線圖。中心表示我們必須達到的最小成本。
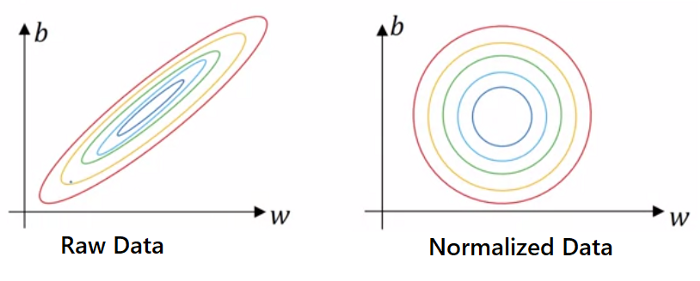
右邊的圖看起來更對稱,這是標準化背後的工作原理的關鍵。
如果特徵的範圍變化很大,則不同權重的值也會隨着發生很大的變化,並且將花費更多的時間來選擇完美的權重集。然而,如果我們使用標準化數據,那麼權重就不會有很大的變化,從而在較短的時間內獲得理想的權重集。
此外,如果使用原始數據,則必須使用較低的學習率來適應不同的等高線高度。但是在歸一化數據的情況下,我們有更多的球面輪廓,通過選擇更大的學習速率,我們可以直接實現最小值。
當特徵在相似的尺度上時,優化權重和偏差變得容易。
梯度消失和梯度爆炸
梯度消失和梯度爆炸問題源於權值的初始化。 以上兩個問題都導致網絡的訓練不當和速度較慢問題。正如其名稱所暗示的那樣,當權重消失並最終變得太小時,就會出現梯度消失;然而在梯度爆炸中,權重會爆炸並變得過大。讓我們用一個案例來更好地理解它們。
設 W 是與單位矩陣 I 相近的經初始化的所有層的權重矩陣。
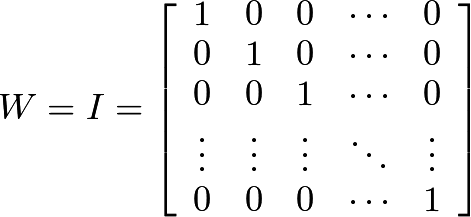
在前向傳播中,一個特定層的輸出 Z 由以下公式定義,其中 W 是權重矩陣,X 是輸入,b 是偏差:
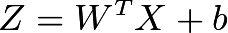
如果我們在 L 層(L 爲層數)上執行上述計算,那麼我們可以假設權重矩陣 W 將乘以 L 次,忽略偏差。
現在,如果特定值大於 1 ,例如 1.5,則層的激活將呈指數遞增,梯度將變大的,與此同時梯度下降將採取大的步長,並且網絡將花費很長時間來達到最小值。這種問題被稱爲梯度爆炸。
同樣的,如果特定值小於 1,例如 0.9,則層的激活將呈指數遞減,梯度將變得很小,與此同時梯度下降將採取小的步長,並且網絡將需要很長時間才能達到最小值。 這種問題被稱爲梯度消失。
爲了避免梯度爆炸和梯度消失的問題,我們應該遵循以下規則 :
1. 激活層的均值應該爲 0
2. 激活層的方差應該在每一層都保持不變。
如果遵循上述規則,則能夠確保梯度下降不會採取太大或太小的步長,並以有序的方式向最小值方向移動,從而避免了梯度爆炸和梯度消失問題。這也意味着網絡將以更快的速度進行訓練和優化。由於問題的根源在於權值的初始化不當,所以我們可以通過正確地初始化權值來解決這個問題。
Xavier 初始化
當特定層的激活函數爲 Tanh 時,則使用 Xavier 初始化。我們可以按照以下方式使用 Xavier 初始化:
# Let the dimesnion of weight matrix be(5,3)
# The variance is (1/neurons in previous layer)
# Randn ensure that the mean = 0
W = np.random.randn(5,3) * np.sqrt(1/3))
He 初始化
當特定層的激活函數爲 ReLU 時,可使用 He初始化。我們可以通過以下方式使用 He初始化:
# Let the shape of the weight matrix be(5,3)
# The variance is (2/neurons in previous layer)
# Randn ensure that the mean = 0
W = np.random.randn(5,3) * np.sqrt(2/3))
相關參考:
Deep Learning Notes
Coursera — Deep Learning Course 2
via https://medium.com/analytics-vidhya/optimization-problem-in-deep-neural-networks-400f853af406
本文譯者:Ryan、肖書忠