近日,一篇名爲《A Simple Proof of the Quadratic Formula》的研究出現在了論文預印版發佈平臺 arXiv 上,並獲得了人們的關注。
這篇文章提出了一種二次方程的「極簡」推導方式,這種方法在計算上是輕量級的,其概念也是順應自然的,很有可能會讓全球初中生的二次方程求解過程變得從此不再困難。
而這一簡潔的方法是由美籍華裔數學家、奧賽國家隊總教練羅博深發現的。

二次方程式是古人在數學上探索的重要成就之一,其歷史可以追溯到公元前 2000 年到 1600 年古巴比倫時期。在超過 4000 年的歷史中,不少著名數學家都「重新發現」了其求解方法。
當然對於絕大多數人來說,二次方程求解公式是今天代數第一階段課程的標準部分。
然而不幸的是,對於數以十億計的全球人民來說,二次公式是必須記下來的第一個複雜公式(有可能也是唯一一個),這就是我們都必須學的韋達定理:
設一元二次方程 ax^2+bx+c=0(abc 爲實數,a≠0)兩根 x_1、x_2 有如下關係,
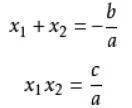
由一元二次方程求根公式可知
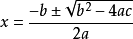
和高中、大學期間我們會學到的很多數學公式相比,這一方法雖然算得上簡單,但它依賴於另一種基本的數學技巧「配方法」,而遠非直覺。
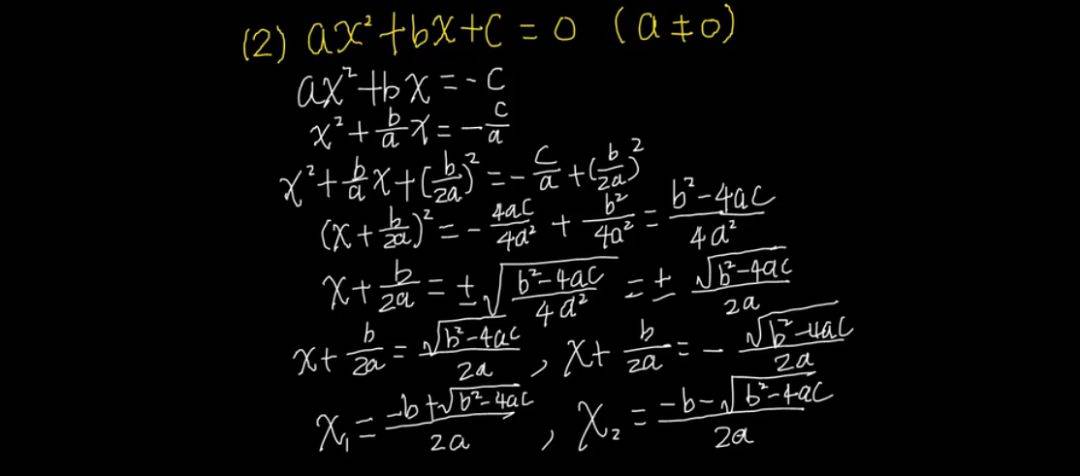
所以在古巴比倫人首次提出之後,數學家們花費了幾個世紀才偶然發現了這一證明。在這之前和之後,有很多其他的推導公式出現,但所有方式看起來都是複雜和「反人類」的。
羅博深找到了一個令人驚訝的二次方程推導方式,由此還產生了一種求解一般二次方程式的高效、自然且易於記憶的算法。
考慮到這一課題已經有 4000 多年曆史,並被數十億人接觸過,直到今天才被才發現的確是非常令人驚訝的一件事。
羅博深的方法不依賴於配方,或任何其他相對困難的數學技巧。它非常簡單,可用作通用方法,讓學生們拋棄現在的公式。這種方法的推導過程是這樣的:
假設二次方程式有兩個根 R 和 S,和上面的經典方法一樣,我們可將其寫作,
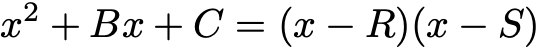
當 x=R 或 x=S 時,右側等於零。將右邊拆開得,
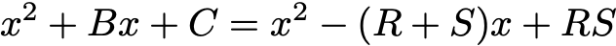
所以-B=R+S 且 C=RS 時,等式成立,
現在到了有趣的地方,羅博深指出,這個時候 R 和 S 的和是-B,所以二次方程兩個根的平均值就是-B/2。「所以我們要求根,就是在找-B/2±z,其中的 z 是單個未知量。」(當然如果 z 是零,則 R=S=-B/2)。因爲 C=RS,所以;
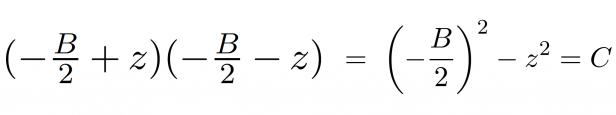
整理後得,
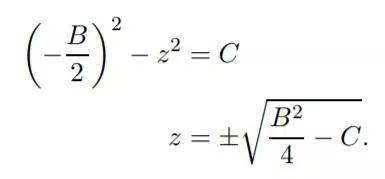
所以二次方程的解就是,
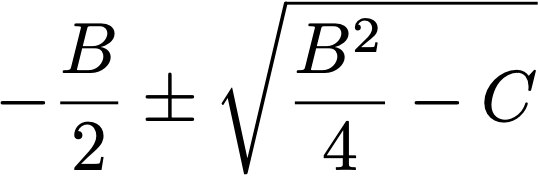
看起來也不簡單?不過實際上與以前的方法相比,這個新方法有一些重要的改進。羅博深舉了一個例子來進行了解釋。
求解這個方程,x^2-2x+4=0:
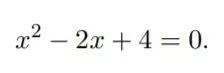
傳統方法是根據方程裏 a、b 和 c 的值,將其帶入經典公式然後求解。而在新方法上,首先方程的兩個根等於-B/2±z,也就是 1±z;
且兩個根的乘積是 C=4,因此:
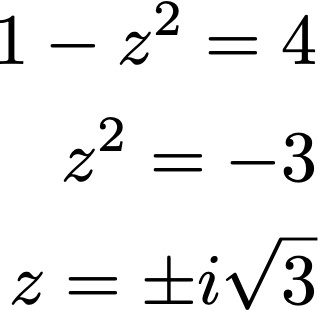
因此方程的根爲 1±i√3
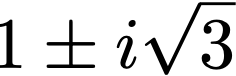
無理數和虛數毫無壓力。大家可以嘗試用傳統方法來解一下這個方程,肯定會難得多。

論文鏈接:https://arxiv.org/abs/1910.06709
在一個「簡單」問題上找到了一個新的、更好的解法,這真的是人類的第一次發現嗎?前不久陶哲軒等人求解特徵值向量的研究《Eigenvectors from Eigenvalues》,在令人興奮的發表之後,還被認爲是「重複造輪子」。對此羅博深對自己提出方法的原創性進行了一番探討。
簡而言之,他研究了有關數學歷史的大量文獻,包括古巴比倫人、中國人、希臘人、印度人和阿拉伯人以及從文藝復興時期到今天的現代數學家提出的方法,想要尋找前人發現過的可能性,然而並沒有成功。
看起來,我們有了一個全新的二次方程求解方法。

發現這一方法的華裔學者羅博深(Po-Shen Loh)不僅是 CMU 的一名數學教授,還是一名社會活動家,致力於全球數學教育的研究。此外,他還是免費個性化學習平臺 expii.com 的創始人。這位學者目前擔任美國國際數學奧林匹克隊的總教練。
羅博深 2004 年本科畢業於加州理工州立大學,在 2005 年獲得劍橋大學數學碩士學位。在學術和競賽方面,羅博深也曾獲得過不少榮譽,包含國際數學奧林匹克銀牌、總統科學家和工程師早期職業獎(PECASE)。他的研究領域包含離散系統、概率論和計算機科學交叉領域等方向。