在深度學習模型的優化上，梯度下降並非唯一的選擇

雷鋒網AI科技評論按：如果你是一名機器學習從業者，一定不會對基於梯度下降的優化方法感到陌生。對於很多人來說，有了 SGD，Adam，Admm 等算法的開源實現，似乎自己並不用再過多關注優化求解的細節。然而在模型的優化上，梯度下降並非唯一的選擇，甚至在很多複雜的優化求解場景下，一些非梯度優化方法反而更具有優勢。而在衆多非梯度優化方法中，演化策略可謂最耀眼的那顆星！

對於深度學習模型的優化問題來說，隨機梯度下降（SGD）是一種被廣爲使用方法。然而，實際上 SGD 並非我們唯一的選擇。當我們使用一個「黑盒算法」時，即使不知道目標函數 f(x):Rn→R 的精確解析形式（因此不能計算梯度或 Hessian 矩陣）你也可以對 f(x) 進行評估。經典的黑盒優化方法包括「模擬退火算法」、「爬山法」以及「單純形法」。演化策略（ES）是一類誕生於演化算法（EA）黑盒優化算法。在本文中，我們將深入分析一些經典的演化策略方法，並介紹演化策略在深度強化學習中的一些應用。

目錄

一、演化策略是什麼？

二、 簡單的高斯演化策略

三、協方差矩陣自適應演化策略（CMA-ES）

1、均值更新

2、步長控制

3、協方差自適應

四、自然演化策略（NES）

1、自然梯度

2、使用費舍爾（Fisher）信息矩陣進行估計

3、NES 算法

五、應用：深度強化學習中的演化策略

1、OpenAI 用於強化學習的演化策略

2、演化策略的探索方式

3、 CEM-RL：結合演化策略和梯度下降方法的強化學習策略搜索

六、擴展：深度學習中的演化策略

1、超參數調優：PBT

2、網絡拓撲優化：WANN

七、參考文獻

一、演化策略是什麼？

演化策略（ES）從屬於演化算法的大家族。ES 的優化目標是實數向量 x∈Rⁿ。

演化算法（EA）指的是受自然選擇啓發而產生的一類基於種羣的優化算法。自然選擇學說認爲，如果某些個體具有利於他們生存的特性，那麼他們就可能會繁衍幾代，並且將這種優良的特性傳給下一代。演化是在選擇的過程中逐漸發生的，整個種羣會漸漸更好地適應環境。

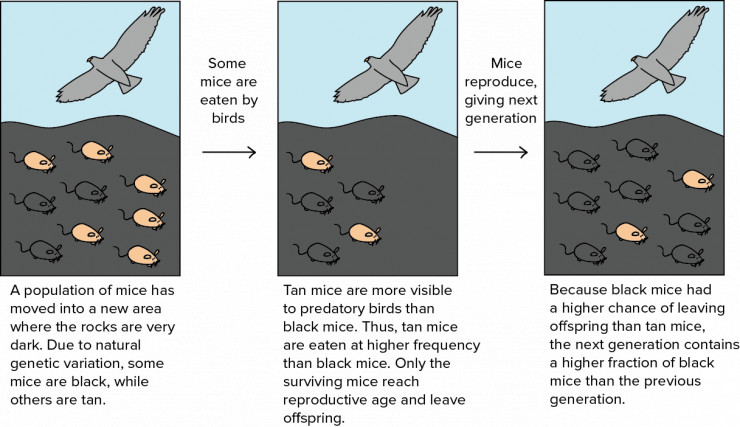
圖 1：自然選擇工作原理示意圖（圖片來源：可汗學院「達爾文、進化與自然選擇」：https://www.khanacademy.org/science/biology/her/evolution-and-natural-selection/a/darwin-evolution-natural-selection）。

（左）一羣老鼠移動到了一個岩石顏色非常暗的地區。由於自然遺傳的變異，有些老鼠毛色是黑色，有的則是棕褐色。（中）相較於黑色的老鼠來說，棕褐色的老師更容易被肉食性鳥類發現。因此，褐色老鼠比黑色老鼠更頻繁地被鳥類捕食。只有存活下來的老鼠到了生育年齡後會留下後代。（右）由於黑色老鼠比褐色老鼠留下後代的機會更大，在下一代老鼠中黑色的佔比上一代更高。

我們可以通過以下方式將演化算法概括爲一種通用的優化方案：

假設我們想要優化一個函數 f(x)，而且無法直接計算梯度。但是，我們在給定任意 x 的情況下仍然可以評估 f(x)，而且得到確定性的結果。我們認爲隨機變量 x 的概率分佈 p_θ(x) 是函數 f(x) 優化問題的一個較優的解，θ 是分佈 p_θ(x) 的參數。目標是找到 θ 的最優設置。

在給定固定分佈形式（例如，高斯分佈）的情況下，參數 θ 包含了最優解的知識，在一代與一代間進行迭代更新。

假設初始值爲 θ，我們可以通過循環進行下面的三個步驟持續更新 θ：

• 1. 生成一個樣本的種羣 D={(x_i,f(x_i)}，其中 x_i∼p_θ(x)。

• 2. 估計 D 中樣本的「適應度」。

• 3. 根據適應度或排序，選擇最優的個體子集，並使用它們來更新 θ。

在遺傳算法（GA，另一種流行的演化算法子類）中，x 是二進制編碼的序列，其中 x∈{0,1}ⁿ。但是在演化策略中，x 僅僅是一個實數向量，x∈Rⁿ。

二、簡單的高斯演化策略

高斯演化策略是最基礎、最經典的演化策略（相關閱讀可參考：http://blog.otoro.net/2017/10/29/visual-evolution-strategies/）。它將 p_θ(x) 建模爲一個 n 維各向同性的高斯分佈，其中 θ 僅僅刻畫均值 μ 和標準差 σ。

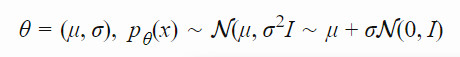
給定 x∈Rⁿ，簡單的高斯演化策略的過程如下：

1. 初始化 θ=θ⁽⁰⁾ 以及演化代數計數器 t=0。

2. 通過從高斯分佈中採樣生成大小爲 Λ 的後代種羣： 

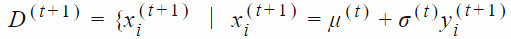
其中，

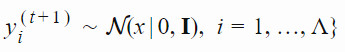
3. 選擇出使得 f(x_i) 最優的 λ 個樣本組成的子集，該子集被稱爲「精英集」。爲了不失一般性，我們可以考慮 D^(t+1) 中適應度排名靠前的 k 個樣本，將它們放入「精英集」。我們可以將其標註爲： 

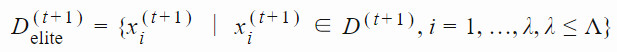
4. 接着，我們使用「精英集」爲下一代種羣估計新的均值和標準差：

 

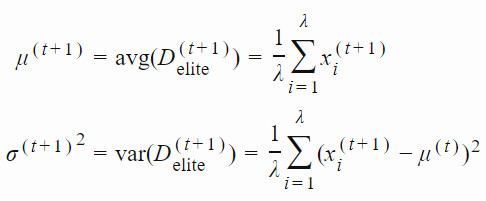
5. 重複步驟 2—步驟 4，直到結果滿足要求。

三、協方差矩陣自適應演化策略（CMA-ES）

標準差 σ 決定了探索的程度：當 σ 越大時，我們就可以在更大的搜索空間中對後代種羣進行採樣。在簡單高斯演化策略中，σ^(t+1) 與 σ^(t) 密切相關，因此算法不能在需要時（即置信度改變時）迅速調整探索空間。

「協方差矩陣自適應演化策略」（CMA-ES）通過使用協方差矩陣 C 跟蹤分佈上得到的樣本兩兩之間的依賴關係，解決了這一問題。新的分佈參數變爲了：

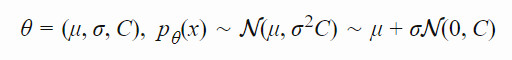
其中，σ 控制分佈的整體尺度，我們通常稱之爲「步長」。

在我們深入研究 CMA-ES 中的參數更新方法前，不妨先回顧一下多元高斯分佈中協方差矩陣的工作原理。作爲一個對稱陣，協方差矩陣 C 有下列良好的性質（詳見「Symmetric Matrices and Eigendecomposition」：http://s3.amazonaws.com/mitsloan-php/wp-faculty/sites/30/2016/12/15032137/Symmetric-Matrices-and-Eigendecomposition.pdf；以及證明：http://control.ucsd.edu/mauricio/courses/mae280a/lecture11.pdf）：

• C 始終是對角陣

• C 始終是半正定矩陣

• 所有的特徵值都是非負實數

• 所有特徵值都是正交的

• C 的特徵向量可以組成 Rn 的一個標準正交基

令矩陣 C 有一個特徵向量 B=[b₁,...,b_n] 組成的標準正交基，相應的特徵值分別爲 λ₁²,…,λ_n²。令 D=diag(λ₁,…,λ_n)。

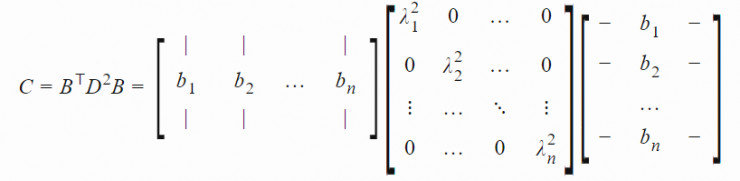
C 的平方根爲：

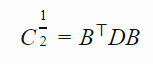
相關的符號和意義如下：

x_i^(t)∈Rⁿ：第 t 代的第 i 個樣本

y_i^(t)∈Rⁿ：x_i^(t)=μ^(t−1)+σ^(t−1)y_i^(t)

μ^(t)：第 t 代的均值

σ^(t)：步長

C^(t)：協方差矩陣

B^(t)：將 C 的特徵向量作爲行向量的矩陣

D^(t)：對角線上的元素爲 C 的特徵值的對角矩陣

p_σ^(t)：第 t 代中用於 σ 的演化路徑

p_c^(t)：第t 代中用於 C 的演化路徑

α_μ：用於更新 μ 的學習率

α_σ：p_σ 的學習率

d_σ：σ 更新的衰減係數

Α_cp：p_c 的學習率

α_cλ：矩陣 C 的秩 min(λ, n) 更新的學習率

α_c1：矩陣 C 的秩 1 更新的學習率

1、更新均值

 

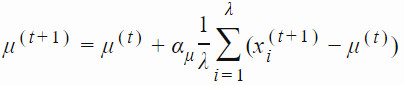
CMA-ES 使用 α_μ≤1 的學習率控制均值 μ 更新的速度。通常情況下，該學習率被設置爲 1，從而使上述等式與簡單高斯演化策略中的均值更新方法相同：

 

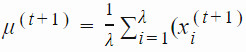
2、控制步長

採樣過程可以與均值和標準差的更新解耦：

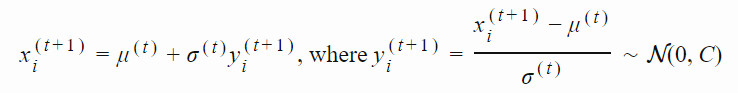
參數 σ 控制着分佈的整體尺度。它是從協方差矩陣中分離出來的，所以我們可以比改變完整的協方差更快地改變步長。步長較大會導致參數更新較快。爲了評估當前的步長是否合適，CMA-ES 通過將連續的移動步長序列相加 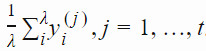，構建了一個演化路徑（evolution path）p_σ。通過比較該路徑與隨機選擇（意味着每一步之間是不相關的）狀態下期望會生成的路徑長度，我們可以相應地調整 σ（詳見圖 2）。

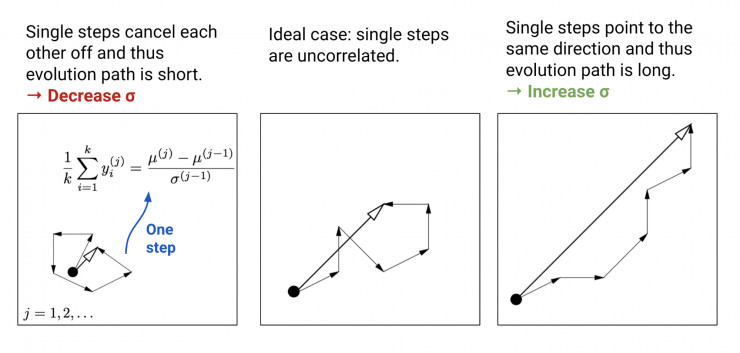
圖 2：將每一步演化以不同的方式關聯起來的三種情況，以及它們對步長更新的影響。（左）每個步驟之間互相抵消，因此演化路徑很短。（中）理想情況：每個步驟之間並不相關。（右）每個步驟指向同一個方向，因此演化路徑較長。（圖片來源：CMA-ES 教程論文中圖 5 的附加註釋，https://arxiv.org/abs/1604.00772）

每次演化路徑都會以同代中的平均移動步長 y_i 進行更新。

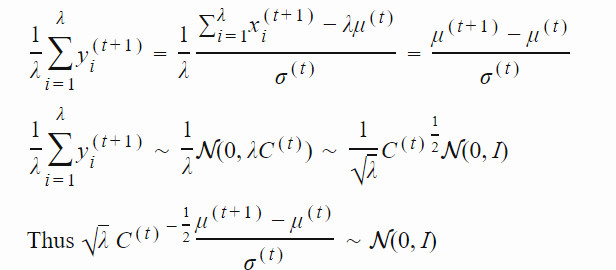
通過與 C^-1/2 相乘，我們將演化路徑轉化爲與其方向相獨立的形式。的工作原理如下：

1. B^(t) 包含 C 的特徵向量的行向量。它將原始空間投影到了正交的主軸上。

2. 將各主軸的長度放縮到相等的狀態。

3. B^(t)⊤將空間轉換回原始座標系。

爲了給最近幾代的種羣賦予更高的權重，我們使用了「Polyak平均 」算法（平均優化算法在參數空間訪問軌跡中的幾個點），以學習率 α_σ 更新演化路徑。同時，我們平衡了權重，從而使p_σ 在更新前和更新後都爲服從 N(0,I)  的共軛分佈（更新前後的先驗分佈和後驗分佈類型相同）。

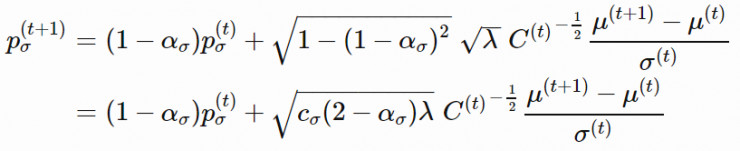
隨機選擇得到的Pσ 的期望長度爲 E‖N(0,I)‖，該值是服從 N(0,I) 的隨機變量的 L2 範數的數學期望。按照圖 2 中的思路，我們將根據 ‖p_σ^(t+1)‖/E‖N(0,I)‖ 的比值調整步長：

 

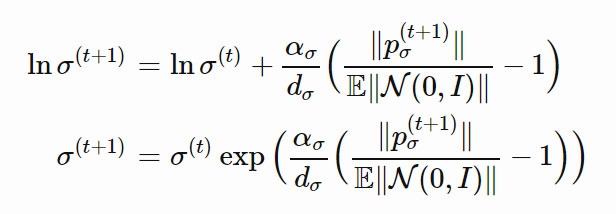
其中，d_σ≈1 是一個衰減參數，用於放縮 ln^σ 被改變的速度。

3、自適應協方差矩陣

我們可以使用精英樣本的 y_i 從頭開始估計協方差矩陣（y_i∼N(0,C)）

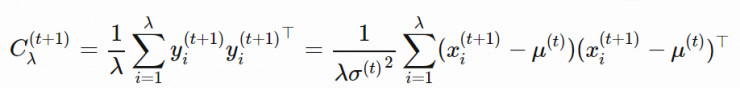
只有當我們選擇出的種羣足夠大，上述估計纔可靠。然而，在每一代中，我們確實希望使用較小的樣本種羣進行快速的迭代。這就是 CMA-ES 發明了一種更加可靠，但同時也更加複雜的方式去更新 C 的原因。它包含兩種獨立的演化路徑：

1. 秩 min(λ, n) 更新：使用 {C_λ} 中的歷史，在每一代中都是從頭開始估計的。

2. 秩 1 更新：根據歷史估計移動步長 y_i 以及符號信息

第一條路徑根據 {C_λ} 的全部歷史考慮 C 的估計。例如，如果我們擁有很多代種羣的經驗，

 

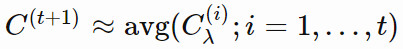
就是一種很好的估計方式。類似於 p_σ，我們也可以使用「polyak」平均，並且通過學習率引入歷史信息：

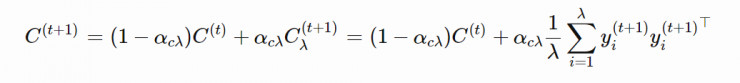
通常我們選擇的學習率爲：

 

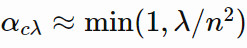
第二條路徑試圖解決 y_iy_i^⊤=(−y_i)(−y_i)^⊤ 丟失符號信息的問題。與我們調整步長 σ 的方法相類似，我們使用了一個演化路徑 p_c 來記錄符號信息，p_c 仍然是種羣更新前後都服從於 N(0,C) 的共軛分佈。

我們可以認爲 p_c 是另一種計算 avg_i(y_i) 的（請注意它們都服從於 N(0,C)），此時我們使用了完整的歷史信息，並且能夠保留符號信息。請注意，在上一節中，我們已經知道了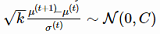，p_c的計算方法如下：

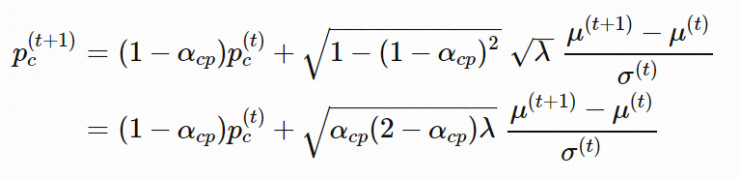
接下來，我們可以根據通過 p_c 更新協方差矩陣：

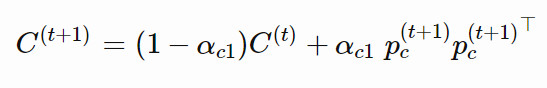
當 k 較小時，秩 1 更新方法相較於秩 min(λ, n) 更新有很大的性能提升。這是因爲我們在這裏利用了移動步長的符號信息和連續步驟之間的相關性，而且這些信息可以隨着種羣的更新被一代一代傳遞下去。

最後，我們將兩種方法結合起來： 

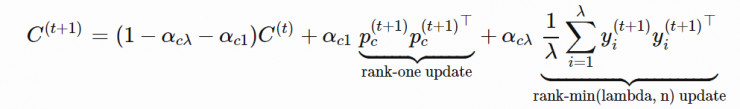
在上面所有的例子中，我們認爲每個優秀的樣本對於權重的貢獻是相等的，都爲 1/λ。該過程可以很容易地被擴展至根據具體表現爲抽樣得到的樣本賦予不同權重 w₁,…,w_λ 的情況。詳情請參閱教程：「The CMA Evolution Strategy: A Tutorial」（https://arxiv.org/abs/1604.00772）

圖 3：CMA-ES 在二維優化問題上的工作原理示意圖（顏色越亮的部分性能越好）。黑點是當前代中的樣本。樣本在初始階段較分散，但當模型在後期較有信心找到較好的解時，樣本在全局最優上變得非常集中。樣本在初始階段較分散，但當模型在後期以更高的置信度找到較好的解時，樣本會集中於全局最優點。

四、自然演化策略

自然演化策略（Wierstra 等人於 2008 年發表的 NES，論文地址：https://arxiv.org/abs/1106.4487）在參數的搜索分佈上進行優化，並將分佈朝着自然梯度所指向的高適應度方向移動。

1、自然梯度

給定一個參數爲 θ 的目標函數 J(θ)，我們的目標是找到最優的 θ，從而最大化目標函數的值。樸素梯度會以當前的 θ 爲起點，在很小的一段歐氏距離內找到最「陡峭」的方向，同時我們會對參數空間施加一些距離的限制。換而言之，我們在 θ 的絕對值發生微小變化的情況下計算出樸素梯度。優化步驟如下：

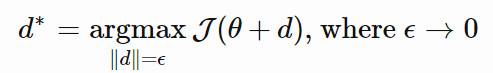
不同的是，自然梯度用到了參數爲 θ, p_θ(x)（在 NES 的原始論文中被稱爲「搜索分佈」，論文鏈接：https://arxiv.org/abs/1106.4487）的概率分佈空間。它在分佈空間中的一小步內尋找最「陡峭」（變化最快）的方向，其中距離由 KL 散度來度量。在這種限制條件下，我們保證了每一步更新都是沿着分佈的流形以恆定的速率移動，不會因爲其曲率而減速。 

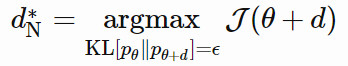
2、使用 Fisher 信息矩陣進行估計

但是，如何精確地計算出 KL[p_θ‖p_θ+Δθ] 呢？通過推導  log_pθ+d 在 θ 處的泰勒展式，我們可以得到：

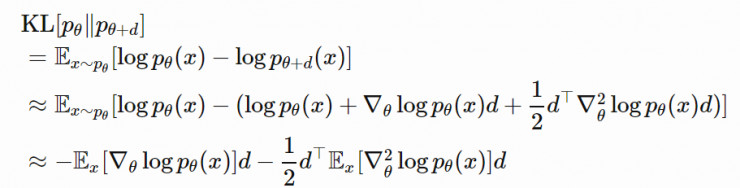
其中，

 

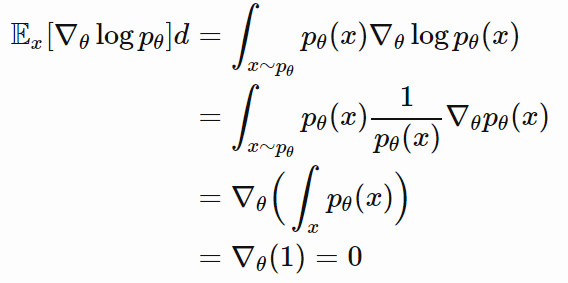
請注意，p_θ(x) 是概率分佈。最終，我們得到了：

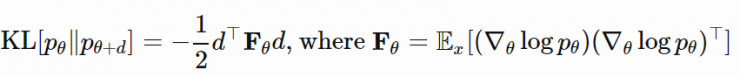
其中，Fθ 被稱爲 Fisher 信息矩陣。由於E[∇_θlogp_θ]=0，所以 Fθ 也是 ∇_θlogp_θ 的協方差矩陣：

針對以下的優化問題： 

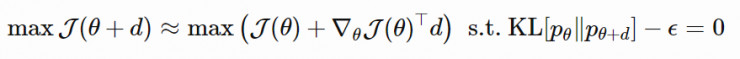
我們可以通過拉格朗日乘子法找到上述問題的解：

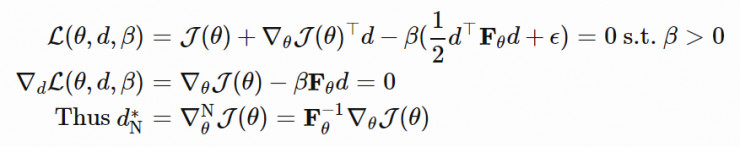其中 d_N^∗僅僅提取了忽略標量 β⁻¹ 的情況下，在 θ 上最優移動步長的方向。

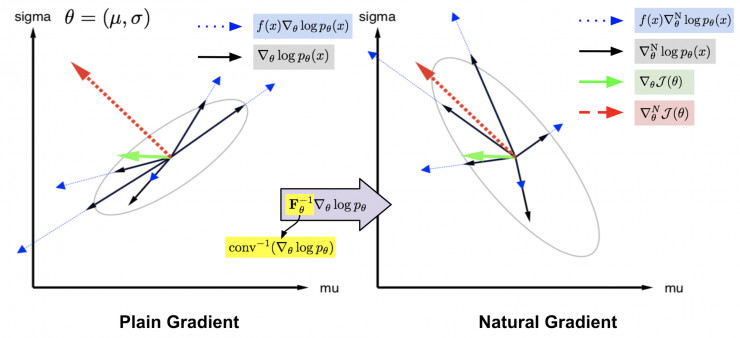
圖 4：右側的自然梯度樣本（黑色實箭頭）是左側的樸素梯度樣本（黑色實箭頭）乘以其協方差的逆的結果。這樣一來，可以用較小的權重懲罰具有高不確定性的梯度方向（由與其它樣本的高協方差表示）。因此，合成的自然梯度（紅色虛箭頭）比原始的自然梯度（綠色虛箭頭）更加可信（圖片來源：NES 原始論文中圖 2 的附加說明，https://arxiv.org/abs/1106.4487）

3、NES 算法

我們將與一個樣本相關聯的適應度標記爲 f(x)，關於 x 的搜索分佈的參數爲 θ。我們希望 NES 能夠優化參數 θ，從而得到最大的期望適應度：

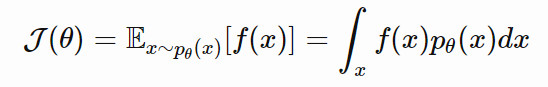
在這裏，我們使用與蒙特卡洛策略梯度強化中相同的似然計算技巧：

除了自然梯度，NES 還採用了一些重要的啓發式方法讓算法的性能更加魯棒。

• NES 應用了基於排序的適應度塑造（Rank-Based Fitness Shaping）算法，即使用適應度值單調遞增的排序結果，而不是直接使用 f(x)。它也可以是對「效用函數」進行排序的函數，我們將其視爲 NES 的一個自由參數。

• NES 採用了適應性採樣（Adaptation Sampling）在運行時調整超參數。當進行 θ→θ′ 的變換時，我們使用曼-惠特尼 U 檢驗（ [Mann-Whitney U-test）對比從分佈 p_θ 上採樣得到的樣本以及從分佈 p_θ′ 上採樣得到的樣本。如果出現正或負符號，則目標超參數將減少或增加一個乘法常數。請注意，樣本 x_i′∼p_θ′(x) 的得分使用了重要性採樣權重 w_i′=p_θ(x)/p_θ′(x)。

五、應用：深度強化學習中的演化策略

1、OpenAI 用於強化學習的演化策略

將演化算法應用於強化學習的想法可以追溯到很久以前的論文「Evolutionary Algorithms for Reinforcement Learning」（論文地址：https://arxiv.org/abs/1106.0221），但是由於計算上的限制，這種嘗試僅僅止步於「表格式」強化學習（例如，Q-learning）。

受到 NES 的啓發，OpenAI 的研究人員（詳見 Salimans 等人於 2017 年發表的論文「Evolution Strategies as a Scalable Alternative to Reinforcement Learning」，論文鏈接：https://arxiv.org/abs/1703.03864）提出使用 NES 作爲一種非梯度黑盒優化器，從而尋找能夠最大化返回函數 F(θ) 的最優策略參數 θ。

這裏的關鍵是，爲模型參數 θ 加入高斯噪聲 ε，並使用似然技巧將其寫作高斯概率密度函數的梯度。最終，只剩下噪聲項作爲衡量性能的加權標量。

假設當前的參數值爲 θ^（區別於隨機變量 θ）。我們將 θ 的搜索分佈設計爲一個各向同性的多元高斯分佈，其均值爲 θ^，協方差矩陣爲 σ²I 

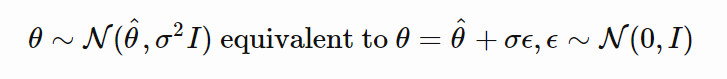
θ 更新的梯度爲：

 

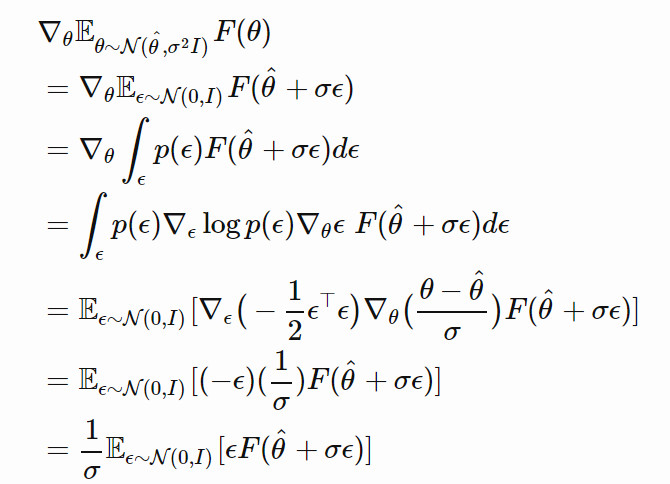
其中，高斯分佈爲。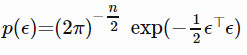

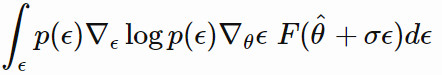是我們用到的似然計算技巧。

在每一代中，我們可以採樣得到許多 ε_i，i=1,…,n，然後並行地估計其適應度。一種優雅的設計方式是，無需共享大型模型參數。只需要在各個工作線程之間傳遞隨機種子，就足以事主線程節點進行參數更新。隨後，這種方法又被拓展成了以自適應的方試學習損失函數。詳情請查閱博文「Evolved Policy Gradient」：

• https://lilianweng.github.io/lil-log/2019/06/23/meta-reinforcement-learning.html#meta-learning-the-loss-function

圖 5：使用演化策略訓練一個強化策略的算法（圖片來源：論文「ES-for-RL」，https://arxiv.org/abs/1703.03864）

爲了使算法的性能更加魯棒，OpenAI ES 採用了虛擬批量歸一化（Virtual BN，用於計算固定統計量的 mini-batch 上的批量歸一化方法），鏡面採樣（Mirror Sampling，採樣一對 (−ϵ,ϵ) 用於估計），以及適應度塑造（Fitness Shaping）技巧。

2、使用演化策略進行探索

在強化學習領域，「探索與利用」是一個很重要的課題。上述演化策略中的優化方向僅僅是從累積返回函數 F(θ) 中提取到的。在不進行顯式探索的情況下，智能體可能會陷入局部最優點。

新穎性搜索（Novelty-Search）演化策略（NS-ES，詳見 Conti 等人於 2018 年發表的論文「Improving Exploration in Evolution Strategies for Deep Reinforcement Learning via a Population of Novelty-Seeking Agents」，論文地址：https://arxiv.org/abs/1712.06560）通過朝着最大化「新穎性得分」的方向更新參數來促進探索。

「新穎性得分」取決於一個針對於特定領域的行爲特徵函數 b(π_θ)。對 b(π_θ) 的選擇取決於特定的任務，並且似乎具有一定的隨機性。例如，在論文裏提到的人形機器人移動任務中，b(π_θ) 是智能體最終的位置 (x,y)。

1. 將每個策略的 b(π_θ) 加入一個存檔集合 A。

2. 通過 b(π_θ) 和 A 中所有其它實體之間的 K 最近鄰得分衡量策略 π_θ 的新穎性。（文檔集合的用例與「情節記憶」很相似）

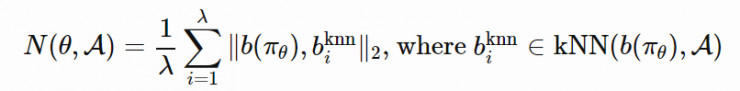
在這裏，演化策略優化步驟依賴於新穎性得分而不是適應度：

 

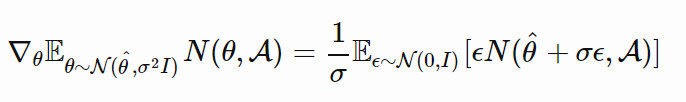
NS-ES 維護了一個由 M 個獨立訓練的智能體組成的集合（「元-種羣」），M={θ₁,…,θ_M}。然後選擇其中的一個智能體，將其按照與新穎性得分成正比的程度演化。最終，我們選擇出最佳策略。這個過程相當於集成，在 SVPG 中也可以看到相同的思想。

 

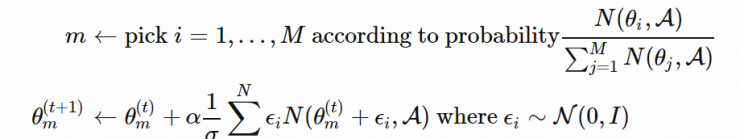
其中，N 是高斯擾動噪聲向量的數量，α 是學習率。

NS-ES 完全捨棄了獎勵函數，僅僅針對新穎性進行優化，從而避免陷入極具迷惑性的局部最優點。爲了將適應度重新考慮到公式中，研究人員又提出了兩種變體。

NSR-ES:

 

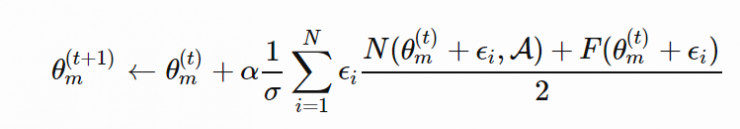
NSRAdapt-ES (NSRA-ES)：自適應的權重參數初始值爲 w=1.0。如果算法的性能經過了很多代之後沒有變化，我們就開始降低 w。然後，當性能開始提升時，我們停止降低 w，反而增大 w。這樣一來，當性能停止提升時，模型更偏向於提升適應度，而不是新穎性。

 

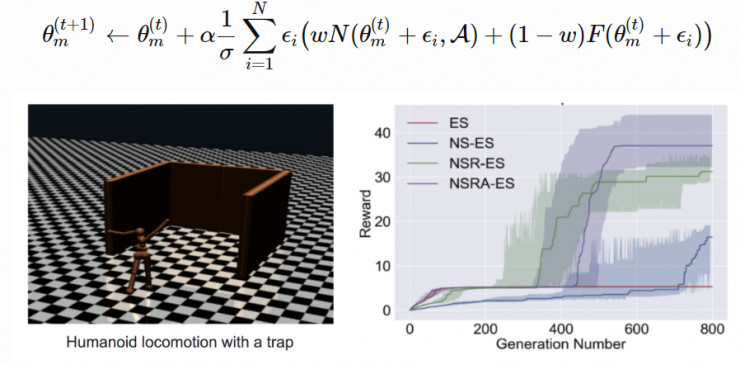
圖 6：（左圖）環境爲人形機器人移動問題，該機器人被困在一個三面環繞的強中，這是一個具有迷惑性的陷阱，創造了一個局部最優點。（右圖）實驗對比了 ES 基線和另一種促進探索的變體。（圖片來源，論文「NS-ES」，https://arxiv.org/abs/1712.06560）

3、CEM-RL

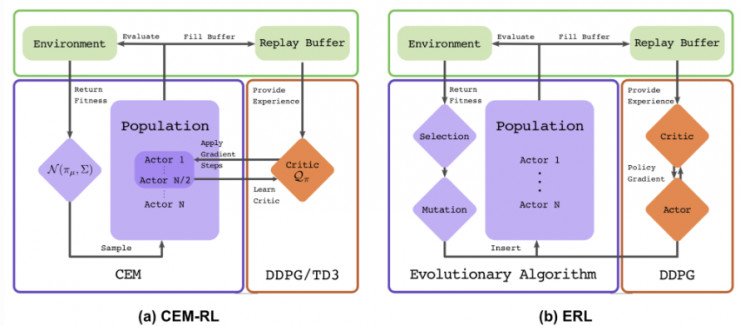
圖 7：CEM-RL 和 ERL 算法（https://papers.nips.cc/paper/7395-evolution-guided-policy-gradient-in-reinforcement-learning.pdf）的架構示意圖（圖片來源：論文「CEM-RL」，https://arxiv.org/abs/1810.01222）

CEM-RL 方法（詳見 Pourchot 和 Sigaud 等人於 2019 年發表的論文「CEM-RL: Combining evolutionary and gradient-based methods for policy search」，論文地址：https://arxiv.org/abs/1810.01222）結合了交叉熵方法（CEM）和 DDPG 或 TD3。

在這裏，CEM 的工作原理與上面介紹的簡單高斯演化策略基本相同，因此可以使用 CMA-ES 替換相同的函數。CEM-RL 是基於演化強化學習（ERL，詳見 Khadka 和 Tumer 等人於 2018 年發表的論文「Evolution-Guided Policy Gradient in Reinforcement Learning」，論文地址：https://papers.nips.cc/paper/7395-evolution-guided-policy-gradient-in-reinforcement-learning.pdf）的框架構建的，它使用標準的演化算法選擇並演化「Actor」的種羣。隨後，在這個過程中生成的首次展示經驗也會被加入到經驗回放池中，用於訓練強化學習的「Actor」網絡和「Critic」網絡。

工作流程：

1. π_μ 爲 CEM 種羣的「Actor」平均值，使用隨機的「Actor」網絡對其進行初始化。

2. 「Critic」網絡 Q 也將被初始化，通過 DDPG/TD3 算法對其進行更新。

3. 重複以下步驟直到滿足要求：

• 在分佈 N(π_μ,Σ) 上採樣得到一個「Actor」的種羣。

• 評估一半「Actor」的種羣。將適應度得分用作累積獎勵 R，並將其加入到經驗回放池中。

• 將另一半「Actor」種羣與「Critic」一同更新。

• 使用性能最佳的優秀樣本計算出新的 π_mu 和 Σ。也可以使用 CMA-ES 進行參數更新。

六、拓展：深度學習中的演化算法

（本章並沒有直接討論演化策略，但仍然是非常有趣的相關閱讀材料。）

演化算法已經被應用於各種各樣的深度學習問題中。「POET」（詳見 Wang 等人於 2019 年發表的論文「Paired Open-Ended Trailblazer (POET): Endlessly Generating Increasingly Complex and Diverse Learning Environments and Their Solutions」，論文地址：https://arxiv.org/abs/1901.01753）就是一種基於演化算法的框架，它試圖在解決問題的同時生成各種各樣不同的任務。關於 POET 的詳細介紹請參閱下面這篇關於元強化學習的博文：https://lilianweng.github.io/lil-log/2019/06/23/meta-reinforcement-learning.html#task-generation-by-domain-randomization。

另一個例子則是演化強化學習（ERL），詳見圖 7（b）。

下面，我將更詳細地介紹兩個應用實例：基於種羣的訓練（PBT），以及權重未知的神經網絡（WANN）

1、超參數調優：PBT

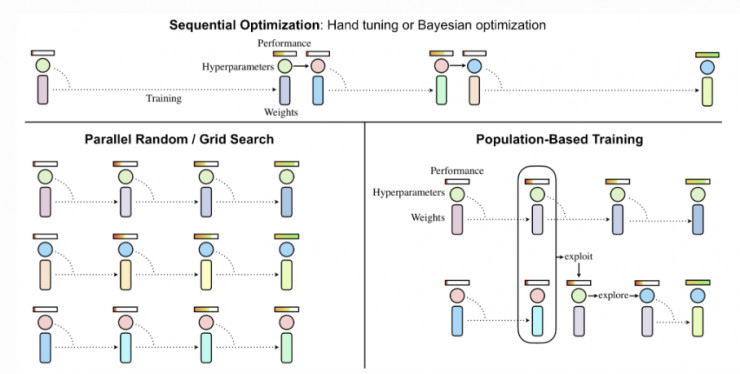
圖 8：對比不同的超參數調優方式的範例（圖片來源：論文「Population Based Training of Neural Networks」，https://arxiv.org/abs/1711.09846）

基於種羣的訓練（PBT，詳見 Jaderberg 等人於 2017 年發表的論文「Population Based Training of Neural Networks」，論文地址：https://arxiv.org/abs/1711.09846）將演化算法應用到了超參數調優問題中。它同時訓練了一個模型的種羣以及相應的超參數，從而得到最優的性能。

PBT 過程起初擁有一組隨機的候選解，它們包含一對模型權重的初始值和超參數 {(θ_i,h_i)∣i=1,…,N}。我們會並行訓練每個樣本，然後週期性地異步評估其自身的性能。當一個成員準備好後（即該成員進行了足夠的梯度更新步驟，或當性能已經足夠好），就有機會通過與整個種羣進行對比進行更新：

• 「exploit()」：當模型性能欠佳時，可以用性能更好的模型的權重來替代當前模型的權重。

• 「explore()」：如果模型權重被重寫，「explore」步驟會使用隨機噪聲擾動超參數。

在這個過程中，只有性能良好的模型和超參數對會存活下來，並繼續演化，從而更好地利用計算資源。

圖 9：基於種羣的訓練算法示意圖。（圖片來源，論文「Population Based Training of Neural Networks」，https://arxiv.org/abs/1711.09846）

2、網絡拓撲優化：WANN

權重未知的神經網絡（WANN，詳見 Gaier 和 Ha 等人於 2019 年發表的論文「Weight Agnostic Neural Networks」，論文地址：https://arxiv.org/abs/1906.04358）在不訓練網絡權重的情況下，通過搜索最小的網絡拓撲來獲得最優性能。

由於不需要考慮網絡權值的最佳配置，WANN 更加強調網絡架構本身，這使得它的重點與神經網絡架構搜索（NAS）不同。WANN 在演化網絡拓撲的時候深深地受到了一種經典的遺傳算法「NEAT」（增廣拓撲的神經演化，詳見 Stanley 和 Miikkulainen 等人於 2002 年發表的論文「Efficient Reinforcement Learning through Evolving Neural Network Topologies」，論文地址：http://nn.cs.utexas.edu/downloads/papers/stanley.gecco02_1.pdf）的啓發。

WANN 的工作流程看上去與標準的遺傳算法基本一致：

1. 初始化：創建一個最小網絡的種羣。

2. 評估：使用共享的權重值進行測試。

3. 排序和選擇：根據性能和複雜度排序。

4. 變異：通過改變最佳的網路來創建新的種羣。

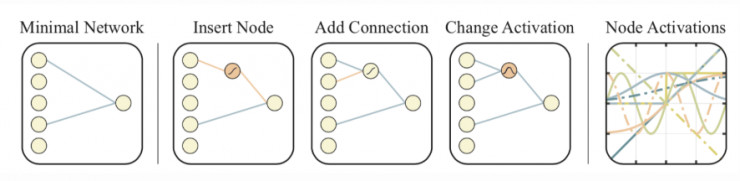
圖 10:：WANN 中用於搜索新網絡拓撲的變異操作。（從左到右分別爲）最小網絡，嵌入節點，增加連接，改變激活值，節點的激活。

在「評估」階段，我們將所有網絡權重設置成相同的值。這樣一來，WANN 實際上是在尋找可以用最小描述長度來描述的網絡。在「選擇」階段，我們同時考慮網絡連接和模型性能。

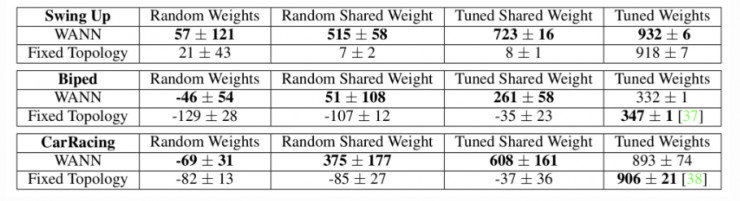
圖 11：將 WANN 發現的網絡拓撲在不同強化學習任務上的性能與常用的基線 FF 網絡進行了比較。「對共享權重調優」只需要調整一個權重值。

如圖 11 所示，WANN 的結果是同時使用隨機權重和共享權重（單一權重）評估得到的。有趣的是，即使在對所有權重執行權重共享並對於這單個參數進行調優的時候，WANN 也可以發現實現非常出色的性能的拓撲。

參考文獻

[1] Nikolaus Hansen. 「The CMA Evolution Strategy: A Tutorial」 arXiv preprint arXiv:1604.00772 (2016).

[2] Marc Toussaint. Slides: 「Introduction to Optimization」

[3] David Ha. 「A Visual Guide to Evolution Strategies」 blog.otoro.net. Oct 2017.

[4] Daan Wierstra, et al. 「Natural evolution strategies.」 IEEE World Congress on Computational Intelligence, 2008.

[5] Agustinus Kristiadi. 「Natural Gradient Descent」 Mar 2018.

[6] Razvan Pascanu & Yoshua Bengio. 「Revisiting Natural Gradient for Deep Networks.」 arXiv preprint arXiv:1301.3584 (2013).

[7] Tim Salimans, et al. 「Evolution strategies as a scalable alternative to reinforcement learning.」 arXiv preprint arXiv:1703.03864 (2017).

[8] Edoardo Conti, et al. 「Improving exploration in evolution strategies for deep reinforcement learning via a population of novelty-seeking agents.」 NIPS. 2018.

[9] Aloïs Pourchot & Olivier Sigaud. 「CEM-RL: Combining evolutionary and gradient-based methods for policy search.」 ICLR 2019.

[10] Shauharda Khadka & Kagan Tumer. 「Evolution-guided policy gradient in reinforcement learning.」 NIPS 2018.

[11] Max Jaderberg, et al. 「Population based training of neural networks.」 arXiv preprint arXiv:1711.09846 (2017).

[12] Adam Gaier & David Ha. 「Weight Agnostic Neural Networks.」 arXiv preprint arXiv:1906.04358 (2019).

 via https://lilianweng.github.io/lil-log/2019/09/05/evolution-strategies.html 雷鋒網 AI 科技評論編譯 雷鋒網(公衆號：雷鋒網)

雷鋒網原創文章，未經授權禁止轉載。詳情見轉載須知。