選自sobolev
參與:Nurhachu Null、蔣思源
本文作者曾介紹一些現代變分推理理論。這些方法經常可用於深度神經網絡並構造深度生成模型(例如 VAE 等),或者使用便於探索的隨機控制來豐富確定性模型。本文介紹了一種隨機計算圖,它將隨機變量分解爲其它隨機變量的組合以避免 BP 算法的隨機性。
所有的這些變分推理的案例都會把計算圖轉換成隨機計算圖,即之前確定的那些結點會變成隨機的。不過在這些結點中做反向傳播的方式並不是簡單與直觀的,本文將介紹一些可能的方法。這次我們會注意到,爲什麼通用的方法會如此糟糕,並且會看到我們在連續的例子中能夠做什麼。
首先,要更加正式的描述一下這個問題。假設近似推理(approximate inference)的學習目標如下:
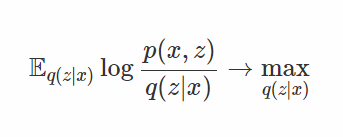
或者是一個強化學習的目標函數:
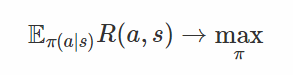
在後面的內容中,我會使用以下標記來表示目標函數:
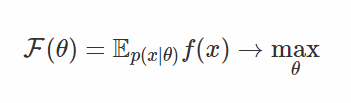
在該情況下,隨機計算圖(SCG)可以被表示成下面的形式 [1]:
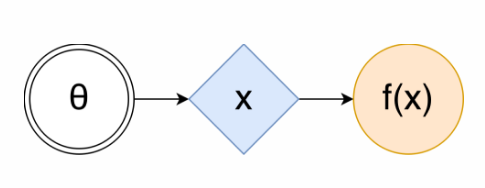
這裏雙層圓環內的θ是可調參數的集合,藍色的菱形是可以取隨機值的隨機點,但是它們的分佈會依賴於θ(或許是通過一些複雜的已知函數來得到,例如神經網絡),橙色的圓圈內的函數 f(x) 是我們要最大化的值。爲了使用這種隨即圖估計得到 F(θ),你只需要使用θ去計算 x 的分佈,我們可能需要儘可能多的樣本爲每一個 x 計算出 f(x),然後再求 f(x) 的均值。
那麼如何最大化它呢?現代深度學習使用的方法是隨機梯度下降(或者是我們例子中使用的梯度上升方法),如果想在我們的例子中應用這種方法,我們所需要做的就是估計(最好具有無偏性和有效性)目標函數關於θ的梯度∇F(θ)。這對任何一個有一定的微積分基礎的人來說是不太難的:
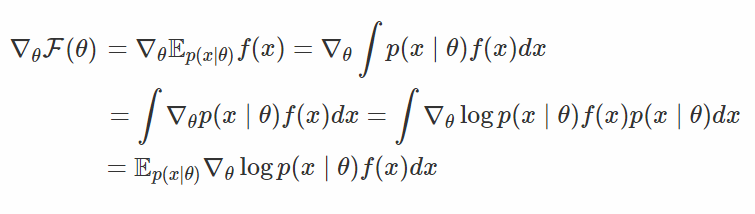
在上式中,我們先採集一些 x 的樣本(x∼p(x∣θ)),並用這些樣本計算得到 f(x),然後將結果和對數密度的梯度相乘,這就是真實梯度的無偏估計了。然而,在實際中人們發現這種估計(被稱作得分函數估計,或者在強化學習文獻中被稱作 REINFORCE)會有較大的方差,會使得對高維的 x 而言不太現實。
注意一下估計器,它並沒有使用 f 的梯度信息,所以它不能給出任何關於如何移動 p(x|θ) 使得 F(θ) 有更高期望的指導。此外,它還使用了很多隨機的 x,對每一個都選擇了應該使得它更有可能的方向,並通過 f(x) 的大小來衡量這些方向。當求取平均值之後,這就會給出一個能夠最大化目標函數的方向,但是很難僅僅使用較少的樣本就能隨機碰到好的 x(尤其是在訓練的早期,或者是在高維空間裏),所以方差會比較大。
這就表現出了對能夠改善這個估計器方差的其他方法的需求,或者是不同的更加有效的估計方法。在下面的內容中我們會給出這兩方面的解釋。
參數重新設置的技巧
當意識到前面提及的侷限性後,Kingm 等人在變分自編碼器的論文中使用了一個聰明的小技巧(https://arxiv.org/abs/1312.6114)。基本思路如下:如果一些隨機變量可以被分解成其他隨機變量的組合,那我們是否能夠將隨機計算圖進行這種分解變換,以避免通過隨機的方式進執行反向傳播,這是否就如同通過獨立的噪聲向模型注入隨機的屬性。
結果是肯定的。也就是說,對於任何高斯隨機變量 x∼N(μ,σ^2),我們都能夠將它分解成一些其他標準高斯噪聲(x=μ+σε,其中 ε∼N(0,1))的仿射變換。我們在這裏重新設定了參數,所以這個技巧就以此命名了。然後隨機計算圖(SCG)就可以表示爲以下形式:
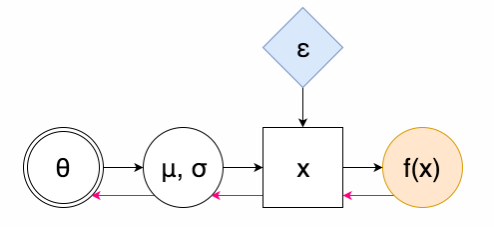
此處紅色的箭頭代表的是反向傳播的「流」:注意我們沒有遇到任何採樣點,所以我們不需要使用高方差得分函數(score-function)估計器。我們甚至可以有很多由隨機單元組成的層級,在參數重設之後我們不需要對所有的樣本做微分,我們只需將它們混合在一起。可以看一下下面的公式:
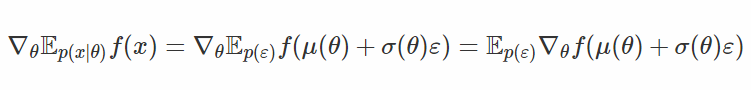
請注意,我們在這裏使用了 f 的梯度!這是這個估計器與得分函數估計器之間最關鍵的不同之處:在後者中,我們利用「分數」隨機的方向進行了平均,同時我們還通過學習得到了一個獨立噪聲的仿射變換,因此經過變換的樣本所在的區域具有較大的 f(x) 值。f 的梯度信息會告訴我們朝着哪裏移動樣本 x,然後我們通過調整 μ 和 δ 來進行這種移動。
這看起來貌似是一個不錯的方法,那麼爲何不在每個地方都是用它呢?問題在於,即使你總能夠將一個均勻分佈的隨機變量變換爲任何其他一個,然而涉及的計算並不總是很容易實現的 [3]。對於某些分佈(例如狄利克雷分佈 [4]),我們甚至不知道任何把無參數隨機變量變換成這種分佈的轉換方法。
泛化的參數重設技巧
參數重設(reparametrization)技巧可以被看成是一種將某些獨立噪聲變成所期望隨機變量的變換 T(ε|θ)。反過來,如果 T 是可逆的,那麼 T(x|θ) 逆就是一個「白噪聲」/「標準噪聲」的變換:它使用一些依賴於參數 θ 的隨機變量,並將它們變成參數獨立的隨機變量。
倘若我們找到的變換方法可能無法將 x 完全變成白噪聲(whiten noise),但是仍然能夠減少它對 θ 的依賴性,那該怎麼辦呢?這就是這篇論文的思想:泛化的參數重設技巧。在那種情況下,ε 仍然依賴於 θ,但是會「弱一些」。
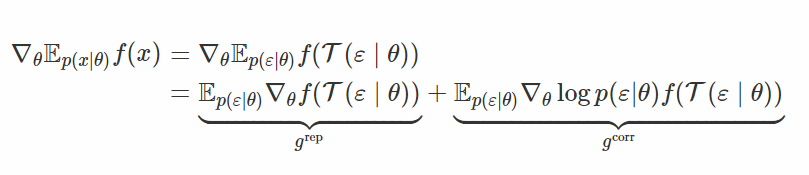
這裏 g^rep 就是我們通常重設參數得到的梯度,g^corr 是得分函數得到的梯度。容易看到,改變變換 T 可以讓你在完全重設參數梯度和完全得分函數梯度之間進行插值(interpolate)。事實上,如果 T 完全將 x 變成白噪聲,那麼 p(ε|θ) 就會獨立於 θ,並且∇logp(ε|θ)=0,我們只能得到 g_rep。但是,如果 T 是一個恆等映射,那麼∇f(T(ε∣θ))=∇f(ε)=0,我們又會恢復到得分函數估計器。
這個公式看起來很棒,但是爲了從中給 ε 進行採樣,我們需要了解 T(x∣θ) 逆的分佈。根據從 p(x|θ) 中的採樣重新用公式表達梯度會更加方便,這個我們可以通過一些代數運算完成:
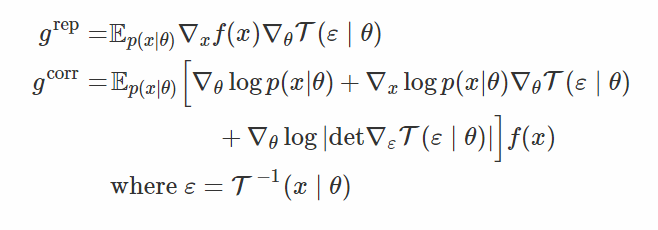
在這個公式中,我們像平常一樣對 x 進行採樣,並把它傳遞到「白化噪聲」變換 T(x|θ) 的逆中,來得到樣本 ε,並在梯度的組成部分中替代這些變量。除了 f(x)∇logp(x∣θ),其他的所有都可以被視爲一個控制變量(我們在後面會討論這個),這個控制變量(control variate)使用 f 的梯度信息,所以它是相當強大的。
最後一個問題是,應該選擇哪個變換?公式的作者建議使用常用的標準變換,即求出平均值,然後再除以標準差。這個選擇是受以下幾點驅動的:a) 計算方便,因爲我們要使用 T 和 T 的逆 [5]; b) 這使得最先的兩個時刻與θ獨立,並從某種程度上導致變量會依賴於 θ。
拒絕採樣(Rejection sampling)的觀點 [6]
另外一個關於泛化參數重設的觀點源於下面的想法:很多分佈都有有效的取樣器,我們能不能在採樣過程中進行反向傳播呢?這正是論文 Reparameterization Gradients through Acceptance-Rejection Sampling Algorithms(通過接受-拒絕算法來進行梯度的參數重設)的作者決定要解決的問題。
你想要對一些分佈 p(x|θ) 進行採樣,但是卻不能計算並翻轉(invert)它的累積分佈函數(CDF),那麼給怎麼辦呢?你可以使用拒絕採樣過程。基本而言,你有一些容易從中採樣的參考分佈 r(x∣θ),然後找到一個縮放因子 M_θ,通過縮放之後,對於所有的 x,參考分佈都要比目標參考的概率密度函數大: M_θr(x|θ)≥p(x|θ)∀x。然後你生成的點都隨機地分佈在 M_θr(x|θ) 曲線的下面,只需要保留(接受)那些同樣分佈在 p(x|θ) 曲線下面的點作爲樣本即可。
1. 生成 x∼r(x|θ)
2. 生成 u∼U[0,M_θr(x|θ)]
3. 如果 u>p(x|θ),從步驟 1 開始重複。否則,返回 x。
此外,我們還對樣本 ε∼r(ε) 使用一些變換 T(ε|θ)(經過縮放的變換變量密度函數會大一些)。這就是 numpy 中生成 Gamma 變量的過程:如果 ε 是標準高斯分佈中的樣本,則通過一些 x=T(ε|θ) 的函數來對樣本進行變換,然後接受服從 a(x|θ) 分佈的樣本即可。[7]
爲了搜索導致接受與 x 對應的 ε 密度函數,我們的變換過程如下:
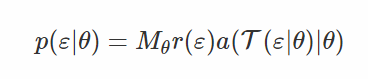
注意,這個概率密度是比較容易計算的,如果我們將生成的樣本 ε 進行參數重設,那麼我們將得到我們所尋找的 x,即 x=T(ε|θ),所以目標函數就可以表示爲:
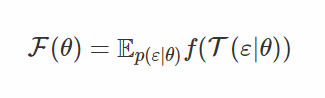
F(θ) 求關於 θ 的梯度,則:
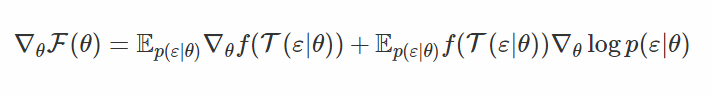
現在我們把後面附加的這一塊與前一部分的 grep 和 gcorr 做一下對比。你會看到它們是完全一樣的!
在前一部分中我們選擇的變換是 T 的逆,因此它一直在試圖去除樣本 x 對θ的依賴。這一部分允許我們從另一方面來觀察同樣的方法:如果你有一些獨立的噪聲 ε 以及一個能讓樣本看起來像是服從目標分佈 p(x|θ) 的變換 T,那麼你可以在上面加一些拒絕採樣來彌補誤採樣,這樣同樣可以得到小方差的梯度估計。
一個非常簡單的例子
讓我們來看一下參數重設的技巧實際上讓方差減小了多少,以一個簡單的問題爲例。我們嘗試將高斯隨機變量平方(x^2)的期望最小化 [8](再加上一些正的常數 c 作爲偏移量,我們會在後面看到它們所起的作用):
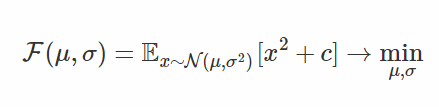
首先,重設參數的目標函數是:
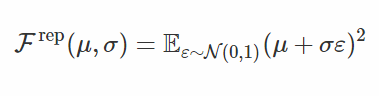
然後它的隨機梯度爲:
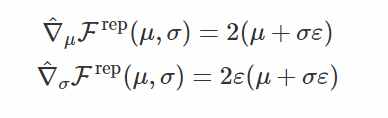
基於得分函數的梯度如下:
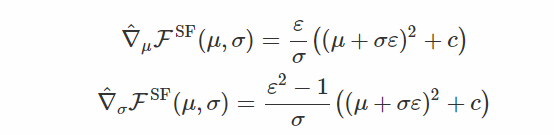
兩個估計器都是無偏估計,但是它們的方差會怎麼樣呢?WolframAlpha 表明:
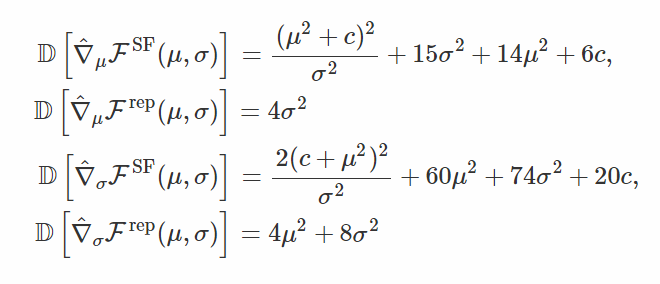
你能夠發現,基於得分函數的梯度不僅方差總是比較大,而且隨着 μ=0、σ=0(除非 c=0,μ足夠小),梯度的方差還會趨於無窮大。這是因爲:隨着方差的變小,採樣點遠離均值的概率會非常小,所以基於得分函數的梯度認爲應該多嘗試讓它們變得更加符合概率分佈。
你也許會好奇,泛化重設參數是如何工作的?如果我們考慮到 [T(x|μ,σ)]^-1=x−μ的逆變換(它僅僅在一階矩進行「白噪聲化處理」),我們將得到以下的梯度估計:
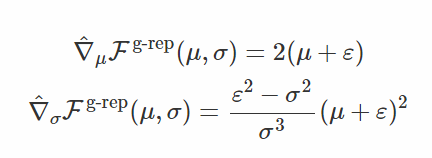
這就是與 μ 對應的參數重設梯度和與 σ 對應的得分函數梯度(這裏 ε∼N(0,σ^2))。我並不認爲這是一個有趣的場景,所以我們會考慮看起來很奇怪的二階矩白噪聲化處理變換 [T(x|μ,σ)]^-1=x−μσ+μ,其中 T(ε|μ,σ)=σ(ϵ−μ)+μ。這種變換下的梯度可以表示如下:
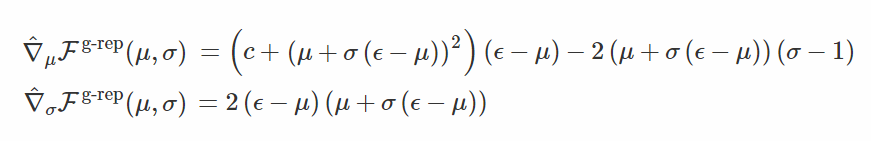
你可以發現,當 σ 接近 0 的時候,梯度的幅值不在趨近於無窮大。讓我們檢查一下這些變量:
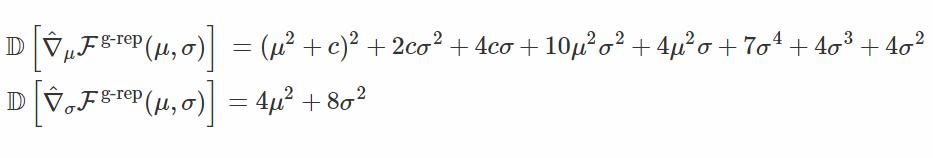
首先,我們可以看到,與 σ 對應的梯度的方差與重設參數的情況下的梯度方差是一樣的。其次,我們可以確定,在接近最優解的時候,梯度的方差不會「爆炸」(趨於無窮大)。
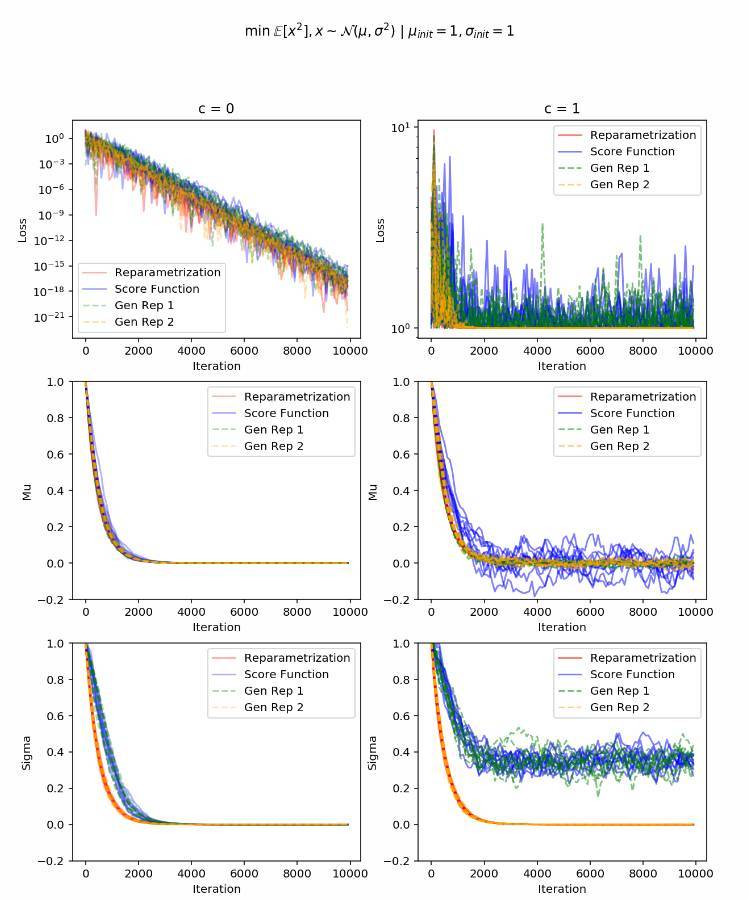
Gen Rep 1 是隻進行了一階矩白噪聲化處理的泛化參數重設。
Gen Rep 2 是隻在二階矩進行了白噪聲化變換處理的泛化參數重設。
模擬曲線清楚地展示:基於得分函數的梯度和第一個泛化參數重設都沒能成功地收斂,這和我們的方差分析是一致的。然而,第二個泛化參數重設則表現得和全參數重設一樣好,即便它的方差還是比較大。
我這篇博文中涉及的工作的源代碼可以在這裏找到(https://gist.github.com/artsobolev/fec7c052d712889ef69656825634c4d4)。但是我要提醒你,代碼相當凌亂。
總結
我們討論了讓隨機變分推理在連續性隱藏變量中變得可計算的技巧。然而,我們往常都是隻對連續的潛在變量模型感興趣。例如,我們可能會對動態選擇一個計算路徑或另一個計算路徑的模型感興趣,這往往要控制在一個給定樣本上花費的計算時間。也許在文本上訓練 GAN 時,我們需要一種在鑑別器的輸入上進行反向傳播的新方式。
原文鏈接:http://artem.sobolev.name/posts/2017-09-10-stochastic-computation-graphs-continuous-case.html
本文爲機器之心編譯,轉載請聯繫本公衆號獲得授權。
責任編輯: