雷鋒網按:本文作者煎魚,原文載於作者個人博客,雷鋒網已獲授權。
寫在前面:囫圇吞棗看完SVM,個人感覺如果不好好理解一些概念,或說如果知其然而不知其所以然的話,不如不看。因此我想隨便寫一寫,把整個思路簡單地整理一遍。: )
SVM與神經網絡
支持向量機並不是神經網絡,這兩個完全是兩條不一樣的路吧。不過詳細來說,線性SVM的計算部分就像一個單層的神經網絡一樣,而非線性SVM就完全和神經網絡不一樣了(是的沒錯,現實生活中大多問題是非線性的),詳情可以參考知乎答案。
這兩個冤家一直不爭上下,最近基於神經網絡的深度學習因爲AlphaGo等熱門時事,促使神經網絡的熱度達到了空前最高。畢竟,深度學習那樣的多層隱含層的結構,猶如一個黑盒子,一個學習能力極強的潘多拉盒子。有人或許就覺得這就是我們真正的神經網絡,我們不知道它那數以百千計的神經元幹了什麼,也不理解爲何如此的結構能誕生如此美好的數據 —— 猶如複雜性科學般,處於高層的我們並不能知道底層的」愚羣「爲何能涌現。兩者一比起來,SVM似乎也沒有深度學習等那麼令人狂熱,連Hinton都開玩笑說SVM不過是淺度學習(來自深度學習的調侃)。
不然,個人覺得相對於熱衷於隱含層的神經網絡,具有深厚的數學理論的SVM更值得讓我們研究。SVM背後偉大的數學理論基礎可以說是現今人類的偉大數學成就,因此SVM的解釋性也非神經網絡可比,可以說,它的數學理論讓它充滿了理性,這樣的理性是一個理工科生嚮往的。就如,你渴望知道食物的來源以確定食物是否有毒,如果有毒是什麼毒,這樣的毒會在人體內發生了什麼反應以致於讓你不適 —— 我的理性驅使我這麼想,一個來路不明的食物是不能讓我輕易接受的。
SVM是什麼
簡單點講,SVM 就是個分類器,它用於迴歸的時候稱爲SVR(Support Vector Regression),SVM和SVR本質上都一樣。下圖就是SVM分類:
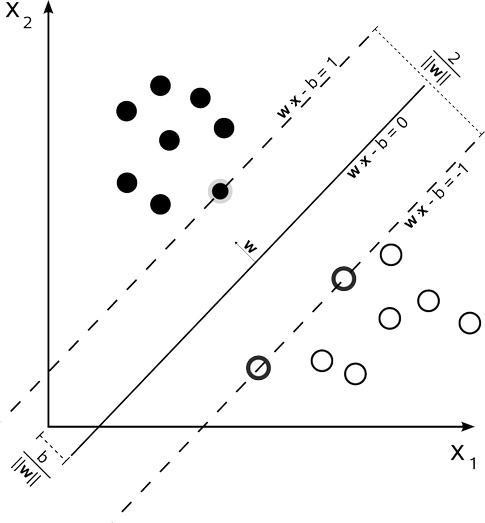
(邊界上的點就是支持向量,這些點很關鍵,這也是」支持向量機「命名的由來)
SVM的目的:尋找到一個超平面使樣本分成兩類,並且間隔最大。而我們求得的w就代表着我們需要尋找的超平面的係數。
用數學語言描述:
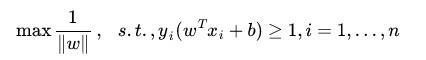
這就是SVM的基本型。
SVM的基本型在運籌學裏面屬於二次規劃問題,而且是凸二次規劃問題(convex quadratic programming)。
二次規劃
二次規劃的問題主要用於求最優化的問題,從SVM的求解公式也很容易看出來,我們的確要求最優解。
簡介:
在限制條件爲
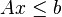
的條件下,找一個n 維的向量 x ,使得
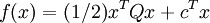
爲最小。
其中,c爲n 維的向量,Q爲n × n 維的對稱矩陣,A爲m × n 維的矩陣,b爲m 維的向量。
其中,根據優化理論,如果要到達最優的話,就要符合KKT條件(Karush-Kuhn-Tucker)。
KKT
KKT是在滿足一些有規則的條件下,一個非線性規則問題能有最優解的一個充分必要條件。也就是說,只要約束條件按照這個KKT給出的規則列出,然後符合KKT條件的,就可以有最優解。這是一個廣義化拉格朗日乘數的成果。
把所有的不等式約束、等式約束和目標函數全部寫爲一個式子:
L(a, b, x)= f(x) + a*g(x)+b*h(x)
KKT條件是說最優值必須滿足以下條件:
● L(a, b, x)對x求導爲零
● h(x) = 0
● a*g(x) = 0
對偶問題
將一個原始問題轉換爲一個對偶問題,懂的人知道對偶問題不過是把原始問題換了一種問法,從另一角度來求問題的解,其本質上是一樣的。就好像我不能證明我比百分之五的人醜,但是我能證明我比百分之九十五的人帥,那樣就夠了。那麼,爲啥要用對偶問題,直接求原始問題不好嗎?參考一下爲什麼我們要考慮線性規劃的對偶問題?
而二次規劃的對偶問題也是二次規劃,性質、解法和原來一樣,所以請放心。(只做簡要介紹)
最後訓練完成時,大部分的訓練樣本都不需要保留,最終只會保留支持向量。這一點我們從圖上也能看得出來,我們要確定的超平面只和支持向量有關不是嗎?
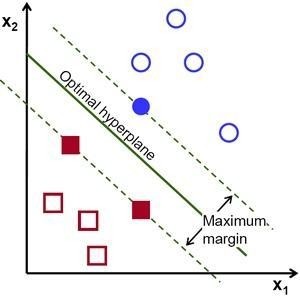
(你看,只和支持向量有關)
然而,問題又出現了(新解法的出現總是因爲新問題的出現),對於SVM的對偶問題,通過二次規劃算法來求解的計算規模和訓練樣本成正比,開銷太大。換句話來說,輸入數據小的時候還好,不過小數據幾乎沒啥用,但是數據量大起來又計算量太大,所以就得尋找一種適合數據量大而且計算量小的解法,這個就是SMO。
SMO
SMO,Sequential Minimal Optimization,針對SVM對偶問題本身的特性研究出的算法,能有效地提高計算的效率。SMO的思想也很簡單:固定欲求的參數之外的所有參數,然後求出欲求的參數。
例如,以下是最終求得的分類函數,也就是我們SVM的目標:
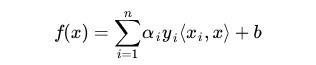
SMO 算法每次迭代只選出兩個分量 ai 和 aj 進行調整,其它分量則保持固定不變,在得到解 ai 和 aj 之後,再用 ai 和 aj 改進其它分量。
如何高效也能通過 SMO 算法的思想看得出來 —— 固定其他參數後,僅優化兩個參數,比起之前優化多個參數的情況,確實高效了。然而,與通常的分解算法比較,它可能需要更多的迭代次數。不過每次迭代的計算量比較小,所以該算法表現出較好的快速收斂性,且不需要存儲核矩陣,也沒有矩陣運算。說白了,這樣的問題用 SMO 算法更好。
核函數
我們的SVM目的其實也簡單,就是找一個超平面,引用一張圖即可表述這個目的:
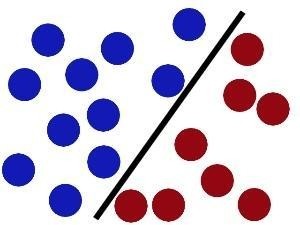
然而現實任務中,原始樣本空間也許並不能存在一個能正確劃分出兩類樣本的超平面,而且這是很經常的事。你說說要是遇到這樣的數據,怎麼劃分好呢:
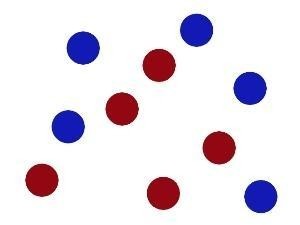
告訴我你的曲線方程吧,傻了吧~
於是引入了一個新的概念:核函數。它可以將樣本從原始空間映射到一個更高維的特質空間中,使得樣本在這個新的高維空間中可以被線性劃分爲兩類,即在空間內線性劃分。這個過程可以觀看視頻感受感受,由於是 youtube 所以我截一下圖:
這是原始數據和原始空間,明顯有紅藍兩類:

通過核函數,將樣本數據映射到更高維的空間(在這裏,是二維映射到三維):

而後進行切割:
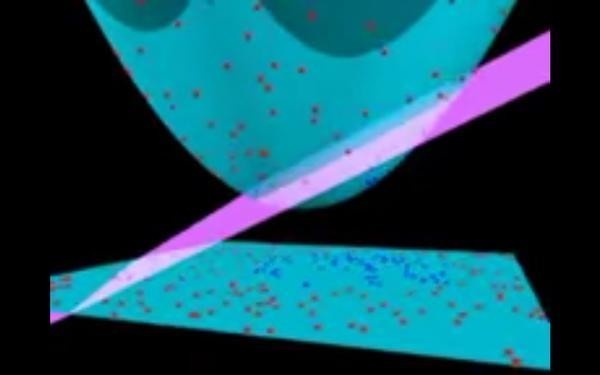
再將分割的超平面映射回去:


大功告成,這些就是核函數的目的。
再進一步,核函數的選擇變成了支持向量機的最大變數(如果必須得用上核函數,即核化),因此選用什麼樣的核函數會影響最後的結果。而最常用的核函數有:線性核、多項式核、高斯核、拉普拉斯核、sigmoid核、通過核函數之間的線性組合或直積等運算得出的新核函數。(這裏只涉及概念,不涉及數學原理)
軟間隔
知道了上面的知識後,你不是就覺得SVM分類就應該是這樣的:
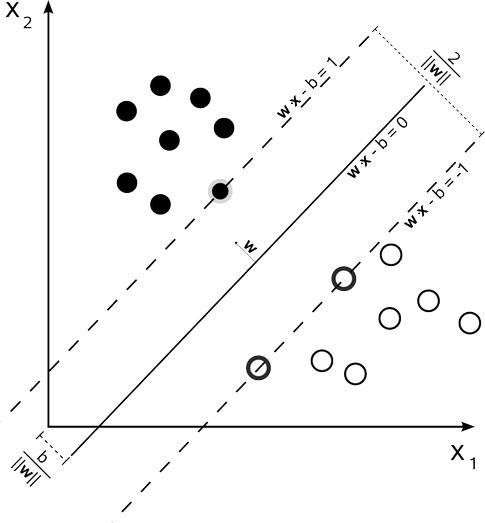
然而這也不一定是這樣的,上圖給出的是一種完美的情況,多麼恰巧地兩類分地很開,多麼幸運地能有一個超平面能將兩個類區分開來!要是這兩個類有一部分摻在一起了,那又該怎麼分啊:
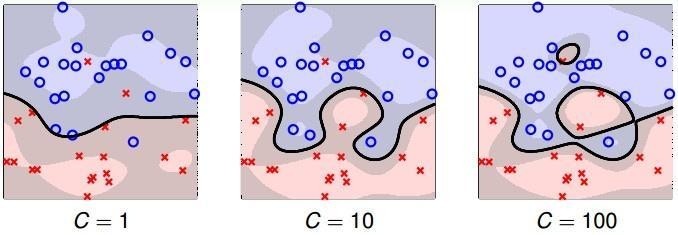
有時候如果你非要很明確地分類,那麼結果就會像右邊的一樣 —— 過擬合。明顯左邊的兩個都比過擬合好多了,可是這樣就要求允許一些樣本不在正確的類上,而且這樣的樣本越少越好,」站錯隊「的樣本數量要通過實際來權衡。這就得用上」軟間隔「,有軟間隔必然有硬間隔,應間隔就是最開始的支持向量機,硬間隔支持向量機只能如此」明確「地分類。特意找來了這個數學解釋:
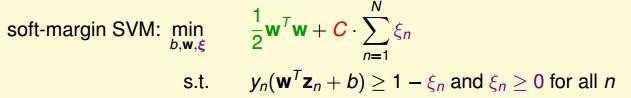
其中一個樣本要是」站錯隊「就要有損失,我們的目的就是:找出總損失值最小並且能大概分類的超平面。而計算一個樣本的損失的損失函數也有很多種,例如:hinge損失、指數損失、対率損失等。
以上只是簡單地把我學習 SVM 的思路整理了一遍,若有錯誤之處還請指正。
雷鋒網(公衆號:雷鋒網)相關閱讀:
基於Spark如何實現SVM算法?這裏有一份詳盡的開發教程(含代碼)
Facebook AI 隊伍再次擴充 聘用業界大拿Vladimir Vapnik
NLP實戰特訓班:阿里IDST9大專家帶你入門
iDST 九大工程師首次在線授課,帶你快速入門NLP技術
課程鏈接:http://m.leiphone.com/special/mooc03