選自arXiv
近日,清華大學段路明組提出一種生成模型的量子算法。在證明因子圖爲量子網絡的特例的基礎上,繼而證明了量子算法在重要應用領域中具備超越任何經典算法的表示能力,可以實現指數級提升,該研究爲量子機器學習開闢了新的研究方向。
論文:An efficient quantum algorithm for generative machine learning

論文地址:https://arxiv.org/abs/1711.02038
量子計算領域的一個核心任務是找到量子計算機可以提供超越傳統計算機實現指數級加速的應用場景。機器學習是一個量子計算機可以在其多個應用層面提供大幅加速的重要領域。針對機器學習的判別式模型,基於線性代數問題的有效求解,人們已發現了多種量子算法,在假設能從量子隨機訪問存儲器中獲取有效輸入的情況下可實現運算的指數級加速。
在機器學習中,生成式模型則代表了另一個大類,其被廣泛用於監督學習和非監督學習。此文中,我們首先提出了量子生成式模型(Quantum Generative Model, QGM)的概念,模型通過測量一系列處於多體糾纏態下的可觀測算符來表示用於描述數據間關係的概率分佈。生成式模型最顯著的特徵是其表徵能力和從數據中學習模型參數的能力,以及對任意變量之間的複雜關係進行推斷的能力。對於表徵能力,我們證明我們提出的 QGM 可以高效地表示任何因子圖(factor graph),其中包括了所有實際應用的經典生成式模型,即經典生成式模型只是 QGM 的特例。此外,通過證明至少存在一些特定的概率分佈,可以被 QGM 表示,但不能被任何使用多項式量級的變量的因子圖進行表示,我們表明 QGM 相對於因子圖具備指數量級的表徵能力(前提是計算複雜度理論中一個被廣泛接受的猜想成立的話,即多項式分層作爲 P vs NP 問題的泛化,是不塌縮的)。
具備表徵能力和泛化能力只是量子生成式模型(QGM)的一個方面,另一方面我們需要可用於訓練和推斷的有效算法。我們提出了一種通用的學習算法,該算法利用對多體糾纏量子態構建的母哈密頓系統(parent Hamiltonian)進行量子相位估計(quantum phase estimation)進行學習。雖然不能期待這種量子算法在所有情況下都能在多項式時間內有效地實現,我們證明了至少存在一些我們的量子算法相對於所有經典算法有指數量級的加速效果的場景。(因爲如果可以證明我們的量子算法在所有情況下都可行,那就意味着量子計算機能高效解決所有 NP 問題,這顯然不太可能)同時這個結論依賴於量子計算機不能被經典計算機高效地模擬這個現在廣爲接受的假設。
我們算法中的指數加速效果可以直觀地理解爲:機器學習生成式模型的目的是通過尋找潛在的概率分佈,對自然界中任意的數據生成過程進行建模。由於自然界是受量子力學定律支配的,所以用經典生成式模型中的概率分佈對現實世界中的數據進行建模,是很有侷限性的。然而,在我們的量子生成式模型中,我們使用一個多體糾纏量子態的概率幅對數據中的相互關係進行參數化。也正是因爲由於量子概率幅的相干性會產生比經典概率模型複雜得多的現象,我們的量子生成式模型也許的確能在特定情況下取得顯著的性能提升。
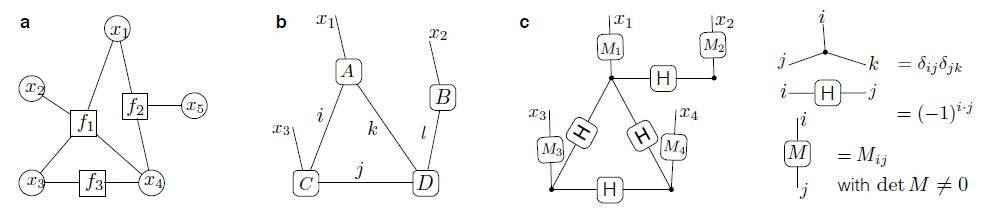
圖 1:經典和量子生成模型。a,因子圖(factor graph)圖示;b,張量網絡狀態(tensor network state)圖示;c,量子生成模型(quantum generative model)定義。
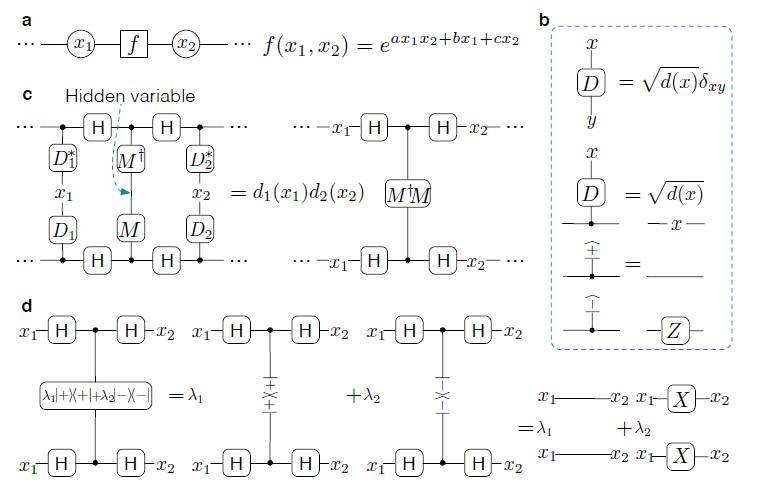
圖 2:通過量子生成模型可以有效表示因子圖。
我們的 QGM 用圖態 |G> 表示,由 m 個量子比特與圖 G(graph G)組成。我們引入下面的變換:
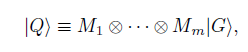
其中 M_i 表示應用在量子比特 i 的 Hilbert 空間上的可逆(通常是非麼正的)2×2 矩陣。從圖 G 的 m 個頂點,我們選擇一個 n 個量子比特的子集作爲可見的單元,並在計算基態 {| 0>;| 1>} 上計算該子集。
從 n 個二元變量 {x_i,i = 1,2, ...,n} 的概率分佈 Q({x_i})中得到計算結果樣本(其他 m×n 個隱藏的量子比特只用來給出低密度矩陣)。給定圖 G 和可見頂點的子集,概率分佈 Q({x_i})定義了由矩陣 Mi 中的參數有效參數化的 QGM。
狀態| Q>可以寫成一個特定的張量網絡狀態(見圖 1)。我們用這種形式來表示我們的模型,原因有二點:首先,概率分佈 Q({x_i})需要具備足以包含所有因子圖的泛化能力; 第二,如果狀態| Q>採取特定的形式,這個模型中的參數可以方便地通過量子算法在數據集上進行訓練。
現在我們證明任何因子圖都可以看成是 QGM 的一個特例,其定理如下:
定理 1:上面定義的 QGM 可以任意高精度地有效表示任何常數度(degree,即節點連接的邊的數量)的因子圖的概率分佈。
定理 2:如果計算複雜性理論中關於多項式分成的泛化假設不塌縮,那麼存在可以被 QGM 高效表示但不能被任何來自由經典生成模型簡化後的因子圖的條件概率有效甚至近似地表示的概率分佈。
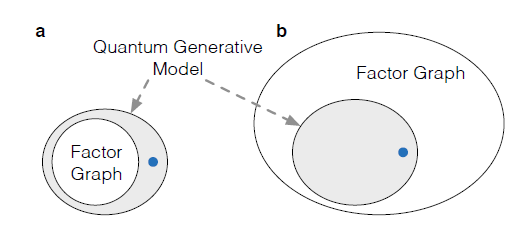
圖 S1:因子圖和 QGM 的參數空間。a,兩種模型都有多項式量級的參數的一種情況。在這種情況下,因子圖不能代表 QGM 中的一些分佈(如藍色圓圈所示處)。b,爲了表示 QGM 中的藍色圓圈的分佈,因子圖必須包含指數級的參數。在這種情況下,參數空間將膨脹到一個非常大的規模。
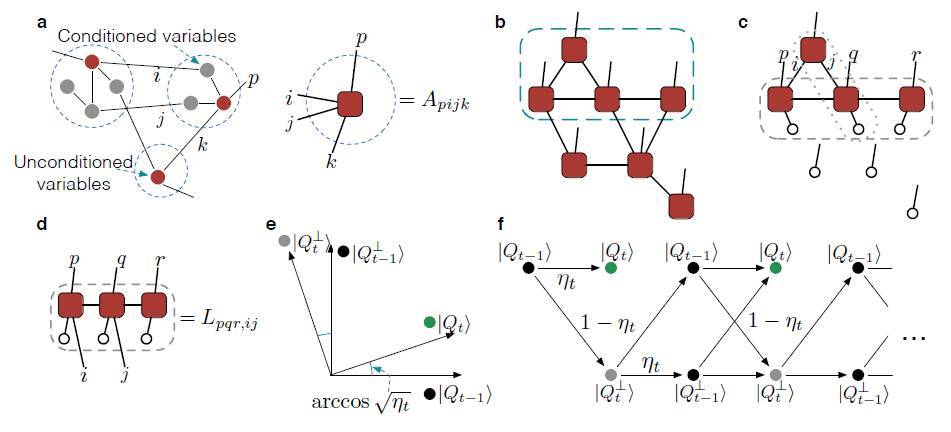
圖 3:關於 QGM 的訓練算法示意圖。
a,QGM 的訓練和推斷過程被簡化到在|Q(z)>狀態下對某些特定操作的測量。因此量子算法的關鍵步驟是獲取狀態|Q(z)>,具體通過針對已構建的母哈密頓系統進行遞歸的量子相位估計的方法制備。
由指定值組成的集合 z 中的變量被稱爲條件變量,而其他標記二元物理索引的變量則被稱爲無條件變量。我們將變量分組,使得每個組只包含一個無條件變量和一些通過少量固定數量的邊連接的不同的組(表示虛擬索引或隱藏變量)。然後每個組使用一個物理索引(用 p 表示)和少量固定數量的虛擬索引(在圖中用 i,j,k 表示)定義一個張量。
b,|Q(z)>的張量網絡表示,其中爲 a 中每個指定的組定義一個局部張量。
c,|Q(t)>的張量網絡表示,其中|Q(t)>是從|Q(z)>簡化的一系列狀態。每一次簡化會移出一個局部張量。移出的局部張量用未填充的圓圈表示,每個圓圈的物理索引設置爲 0. 對於剩餘張量網絡和移出張量之間的邊,我們將相應的虛擬索引設置爲 0(由未填充的圓圈表示)。
d,母哈密頓量(parent Hamiltonian)的構建。該圖顯示瞭如何在母哈密頓算子中構造一個項,該項對應於一組相鄰的局部張量,例如 c 中的虛線框中的那些。在壓縮組內所有虛擬指標之後,我們得到一個張量 L_pqr,ij,其定義了從虛擬指標 i,j 到物理指標 p,q,r 的線性映射 L. 由於指標 i,j 取所有可能的值,該映射 L 的範圍跨越物理指標 p,q,r 的希爾伯特空間 H_p,q,r 中的子空間範圍(L)。該子空間在 H_p,q,r 內部有用 comp(L)表示的互補的正交子空間。
投影到子空間 comp(L),然後在母哈密頓系統中定義一個項,由此定義|Q_t>位於該投影的核空間中。我們用一組相鄰的張量構造每個局部項。每個局部張量可以涉及幾個哈密頓量項(如虛線框和虛線框中的 c 所示),因此一些相鄰組具有非空重疊,並且產生一般不交換的項。通過這種方法,可以構造母哈密頓系統,用其基態來定義狀態|Q_t>。
e,在母哈密頓系統中使用的量子相位估計方法從|Q_t-1>到|Q_t>的演化過程中的狀態的示意圖。|Q_t-1> *,|Q_t> *分別表示在|Q_t-1>和|Q_t>所跨越的二維子空間內正交於|Q_t-1>,|Q_t>的狀態。|Q_t>和|Q_t-1>之間的角度由重疊部分η_t= |
f,通過量子相位估計算法的遞歸應用得到的狀態演化過程。演化過程的每一個分支都是從狀態|Q_t-1>開始,在狀態|Q_t>結束,其中η_t 和 1-η_t 表示相關輸出的概率。
定理 3: 存在計算條件概率和KL 散度的梯度到附加誤差 1/poly(n) 的實例,使得(i)我們的算法可以在多項式時間內得到計算結果;(ii)任何經典算法都不能在多項式時間內完成計算,除非經典計算機能夠高效地模擬量子計算。