選自arXiv
優化技術在科技領域應用廣泛,小到航班表,大到醫療、物理、人工智能的發展,皆可看到其身影,機器學習當然也不例外,且在實踐中經歷了一個從凸優化到非凸優化的轉變,這是因爲後者能更好地捕捉問題結構。本文梳理了這種轉變的過程和歷史,以及從機器學習和信號處理應用中習得的經驗。本文將帶領讀者簡要了解幾種廣泛使用的非凸優化技術及應用,介紹該領域的豐富文獻,使讀者瞭解分析非凸問題的簡單步驟所需的基礎知識。更多詳細內容請查看原論文。
優化作爲一種研究領域在科技中有很多應用。隨着數字計算機的發展和算力的大幅增長,優化對生活的影響也越來越大。今天,小到航班表大到醫療、物理、人工智能的發展,都依賴優化技術的進步。
在這段興奮期的大部分時間,由於我們對凸集合和凸函數的深入瞭解,我們主要聚焦於凸優化問題。但是,信號處理、生物信息學和機器學習等領域的現代應用通常不滿足於僅使用凸函數,因爲非凸公式能夠更好地捕捉問題結構。
近期出現了一些論文開始探討非凸優化,不過第一批論文仍然堅持使用凸優化,致力於證明特定類別的非凸問題(具備與這些問題的自然實例類似的合適結構)可以在沒有損失的前提下轉換成凸問題。更準確地說,原始的非凸問題和修改後的凸問題具備共同的最優解,因此凸問題的解也可以自動解決非凸問題!但是,這種方法需要耗費大量時間解決所謂的鬆弛凸問題(relaxed convex problem)。
第二批論文研究在避免鬆弛凸優化的情況下可證明的非凸優化技術,並用於解決原本形式的非凸問題,似乎取得了與凸鬆弛方法同等質量的結果。伴隨這些較新結果的是新的實現:對於稀疏恢復(sparse recovery)、矩陣補全(matrix completion)、穩健式學習(robust learning)等大量應用,這些直接技術能更快地收斂到最優解,速度通常比基於鬆弛凸優化的技術提高一個數量級甚至更多,而準確率與後者差不多。
本文旨在講述這一實現的歷史,以及從機器學習和信號處理應用的角度中學得的經驗。本文將介紹非凸優化問題和可獲取對此類問題極具擴展性解決方案的大量結構。本文將認真分析和利用額外的任務結構,證明之前避免的 NP-hard 問題現在具備在近線性時間內運行的求解器。本文將告知讀者如何在不同的應用領域查找此類結構,使讀者深入瞭解分析此類問題和提出更新解決方案的基礎工具和概念。
論文: Non-convex Optimization for Machine Learning

論文地址:https://arxiv.org/abs/1712.07897
摘要:大量機器學習算法通過解決優化問題來訓練模型、執行推斷。爲了準確捕捉學習和預測問題,經常出現的稀疏或低秩等結構化約束或目標函數本身都被設計成非凸函數。對運行在高維空間或訓練張量模型和深層網絡等非線性模型的算法尤其如此。
將學習問題表達爲非凸優化問題的便利方式使算法設計者獲得大量的建模能力,但是此類問題通常是 NP-hard 難解決的問題。之前流行的解決方案是將非凸問題近似爲凸優化,使用傳統方法解決近似(凸)優化問題。但是該方法可能造成損失,且對於大規模優化來說難度較高。
另一方面,解決非凸優化的直接方法在多個領域中取得了巨大成功,現在仍是從業者常用的方法,因爲這種方法通常由基於凸鬆弛的技術,流行的啓發式方法包括投影梯度下降(projected gradient descent)和交替最小化(alternating minimization)。但是,人們通常不瞭解其收斂性和其他特性。
本文展示了一些近期進展,這些進展可以填補我們對這些啓發式方法長期以來的認識不足。本文將帶領讀者瞭解幾種廣泛使用的非凸優化技術及應用。本文目標是介紹該領域的豐富文獻,以及使讀者瞭解分析非凸問題的簡單步驟所需的技術。
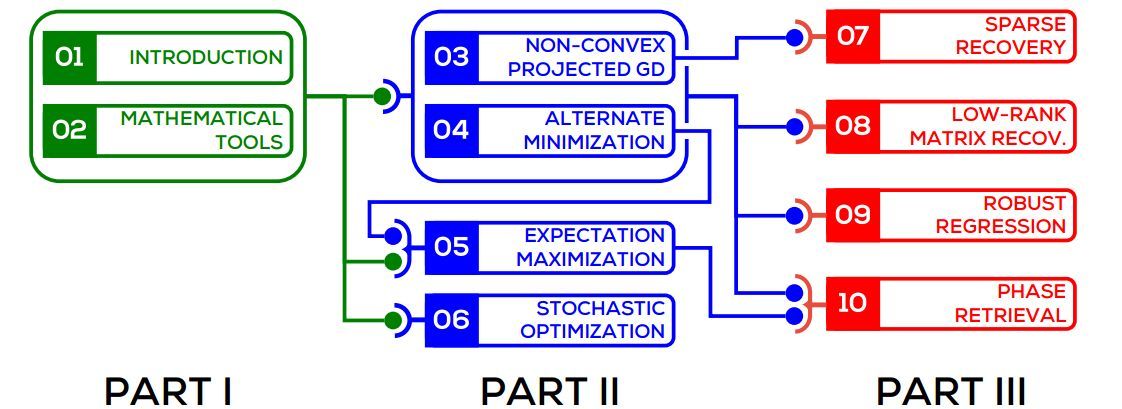
圖 1:章節閱讀建議順序圖示。例如,3、4 章介紹的概念有助於第 9 章的理解,而通讀第 6 章則對此無必要。類似地,我們推薦先讀第 4 章再讀第 5 章,不過讀者可以選擇讀完第 3 章後直接閱讀第 7 章。
第 1 部分:引言和基礎工具。這部分提供介紹性說明和凸優化中的一些基礎概念和算法工具。推薦不熟悉數值優化的讀者閱讀這部分內容。
第 2 部分:非凸優化基元。這部分使讀者瞭解非凸優化問題中最廣泛使用的基元。
第 3 部分:應用。這部分介紹機器學習和信號處理領域中四個有趣的應用,探索如何使用之前介紹的非凸優化技術解決這些問題。
第一章 簡介
這一部分將爲後續討論打下基礎,併爲讀者提供一些非凸優化問題的基本概念與動機,我們將嘗試使用現實生活的案例解釋這些基本概念。
1.1 非凸優化
優化問題的一般形式可以表示爲如下形式:
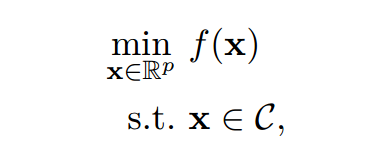
其中 x 爲該優化問題的變量,f:R^p → R 爲該問題的目標函數,C ⊆ R^p 爲優化問題的約束集。當非凸優化應用到機器學習中時,目標函數可以允許算法設計者編碼適當和期望的行爲到機器學習模型中,例如非凸優化中的目標函數可以表示爲衡量擬合訓練數據好壞的損失函數。正如 Goodfellow 所說,一般的非凸優化和深度學習中的非凸優化,最大的區別就是深度學習不能直接最小化性能度量,而只能最小化損失函數以近似度量模型的性能。而對目標函數的約束條件允許約束模型編碼行爲或知識的能力,例如約束模型的大小。
凸優化問題研究的目標函數是凸函數,對應的約束集爲凸集,我們將在第二章正式定義這些術語。一個最優化問題通常會違反一個或多個凸優化條件,即它們通常會有非凸目標函數和非凸約束集等限制,因此這一類的最優化問題可以稱爲非凸優化問題。在本論文中,我們將討論帶有非凸目標函數和非凸約束(§ 4, 5, 6, 8)的非凸優化問題,還有帶有非凸約束和凸目標函數(§ 3, 7, 9, 10, 8)的最優化問題。這些非凸優化的問題在很多應用領域上都有廣泛的體現。
1.2 非凸優化的動機
目前很多應用都頻繁地要求學習算法在極高維度的空間中進行運算。例如網頁文本分類問題就要求基於 n-gram 的表徵有數百萬甚至更高的維度,推薦系統同樣有數百萬的推薦條目和數百萬的推薦用戶,而像人臉識別、圖像分類和生物信息學中的基因檢測等單一處理任務同樣有非常高維度的數據。
處理這種數據和模型需要對模型的學習施加一個結構化約束,這種約束不僅有助於正則化學習問題,同時還經常有助於防止優化問題變得病態。例如如果我們知道用戶如何評價一個推薦條目,那麼我們將希望推斷該用戶將如何評價其它的推薦條目,這通常可以用於廣告推薦中。爲了做到這一點,我們必須明白用戶對一些商品的評價如何影響另一些商品的評價,並針對這種影響添加一些結構化約束。因爲如果沒有這些結構,那麼推斷任何新用戶的評價都是不可能的。正如我們將在下文看到的,這種結構化約束通常都屬於非凸問題。
在其它應用中,學習任務的自然目標函數是非凸函數,特別在深度學習中是高度非凸目標函數。常見的訓練深度神經網絡和張量分解等問題都涉及到本文所述的非凸優化。此外,即使非凸目標函數和約束允許我們準確地建模學習問題,但它們同樣對算法的設計者提出了很嚴峻的挑戰,即如何令高度非凸的目標函數收斂到一個十分理想的近似最優解。非凸優化並不像凸優化,我們並沒有一套便利的工具來解決非凸問題,甚至已知有幾個非凸問題是 NP-hard,我們總是隻能近似地、顯著地減小或增大目標函數的值。由於一系列非凸問題使得最優化變得更加困難,有時候不僅求最優解是 NP-hard,連近似求最優都是 NP-hard [Meka et al., 2008]。
1.4 凸鬆弛方法
面對非凸問題及其與 NP-hard 之間的關係,傳統的解決方案是修改問題的形式化或定義以使用現有工具解決問題。通常通過凸鬆弛來進行,以使非凸問題編碼爲凸問題。由於該方法允許使用類似的算法技術,所謂的凸鬆弛方法得到了廣泛研究。例如,推薦系統和稀疏迴歸問題都應用了凸鬆弛方法。對於稀疏線性迴歸,凸鬆弛方法帶來了流行的 LASSO 迴歸。
現在,這類更改通常給問題帶來巨大改變,鬆弛公式對於原始問題來說不是好的解決方案。但是,如果該問題具備較好的結構,那麼在仔細的鬆弛處理後,這些扭曲(distortion,鬆弛差距)就消失了,即凸鬆弛問題的解也適用於原始的非凸問題。
這種方法很流行也很成功,但是也有侷限性,最顯著的缺點就是可擴展性(scalability)。儘管凸鬆弛優化問題在多項式時間中是可解決的,但在大規模問題中高效地應用這種方法通常比較困難。
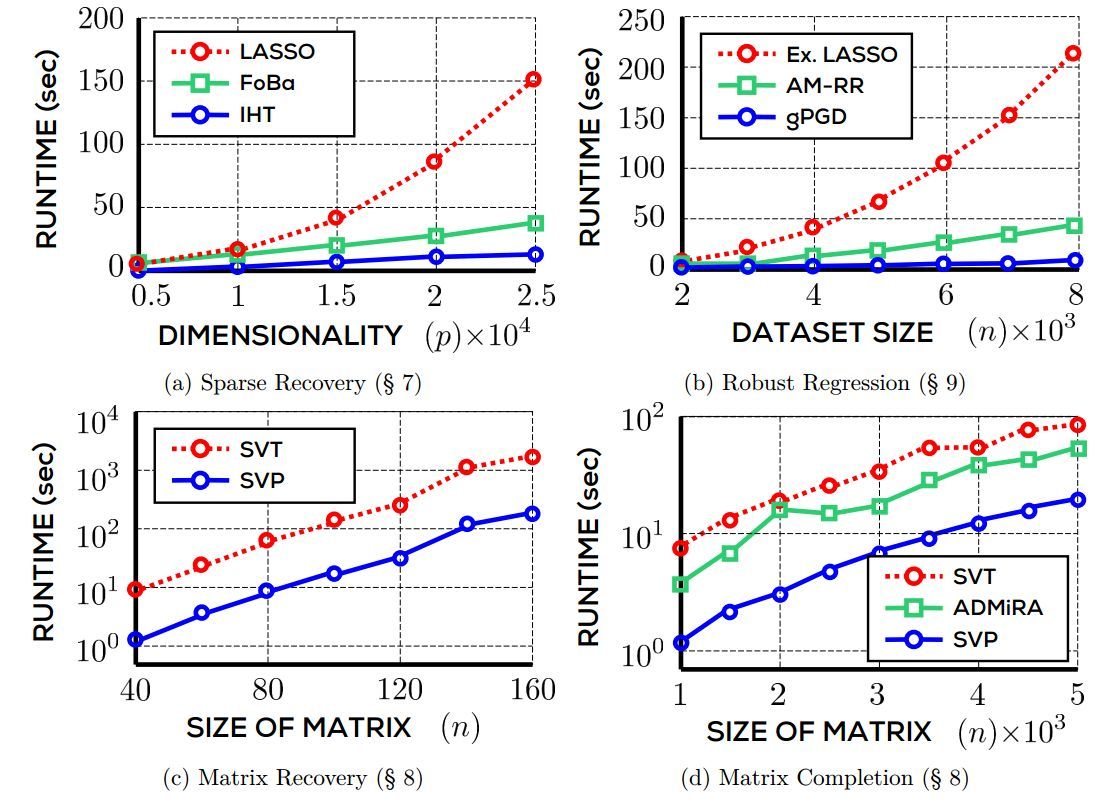
圖 1.3:不同方法在四個非凸優化問題上的運行時實驗對比。LASSO、extended LASSO 和 SVT 是基於鬆弛的方法,IHT、gPGD、FoBa、AM-RR、SVP 和 ADMiRA 是非凸方法。在所有情況中,非凸優化技術比基於鬆弛的方法快出一個數量級。注意圖 1.3c 和 1.3d 使用對數尺度的 y 軸。
1.5 非凸優化方法
有趣的是,近年來,機器學習和信號處理領域出現了一種新方法,不對非凸問題進行鬆弛處理而是直接解決。引起目標是直接優化非凸公式,該方法通常被稱爲非凸優化方法。
非凸優化方法常用的技術包括簡單高效的基元(primitives),如投影梯度下降、交替最小化、期望最大化算法、隨機優化及其變體。這些方法在實踐中速度很快,且仍然是從業者最喜歡用的方法。
但是,最初看來這些方法似乎註定要失敗,因爲前面提到的 NP-hard 問題很難解決。不過,一系列深入、具備啓發性的結果證明了,如果該問題具備較好的結構,那麼不僅可以使用鬆弛方法,還可以使用非凸優化算法。在這類案例中,非凸方法不僅能避免 NP-hard,還可以提供可證明的最優解。事實上,在實踐中它們往往顯著優於基於鬆弛的方法,不管是速度還是可擴展性,見圖 1.3。
非常有趣的一點是,允許非凸方法避免 NP-hard 結果的問題結構與允許圖鬆弛方法避免失真和較大鬆弛差距的結構類似!因此,如果問題具備較好的結構,則基於凸鬆弛的方法和非凸技術都可以成功,但是,非凸技術通常可以提供更具擴展性的解決方案。
第三章 非凸投影梯度下降
本章介紹和研究用於非凸優化問題的梯度下降方法。第 2 章研究了適合解決凸優化問題的投影梯度下降方法。不幸的是,凸問題中使用的這種算法和分析技術不適用於非凸問題。事實上,非凸問題是 NP-hard 的,因此,通常不期望有算法技術可以解決此類問題。
但是,情況並不是那麼糟糕。如第 1 章所討論的,非凸優化的幾個重大突破展示了具備較好額外結構的非凸問題可以在多項式時間中得到有效解決。這裏,我們將研究投影梯度下降方法在此類結構化非凸優化問題上的內部工作原理。
討論分爲三部分。第一部分是約束集,儘管是非凸的,但它們具備額外的結構可使投影高效實施。第二部分是目標函數中幫助優化的結構特性。第三部分是展示和分析適用於非凸問題的 PGD 算法的簡單擴展。我們將看到對於具備較好結構目標函數的問題和約束集,類 PGD 算法可在多項式時間內收斂至全局最優,且收斂速度是線性的。
本章重點是基礎概念的概述和闡釋。我們將試圖用輕鬆、易於理解的方式分析具備非凸目標函數的問題。但是,概述僅限於我們所展示結果的精細度。本章所討論結果不是可能的最優結果,下面的章節中將介紹更精細、更針對特定問題的結果,也會詳細討論特定應用。
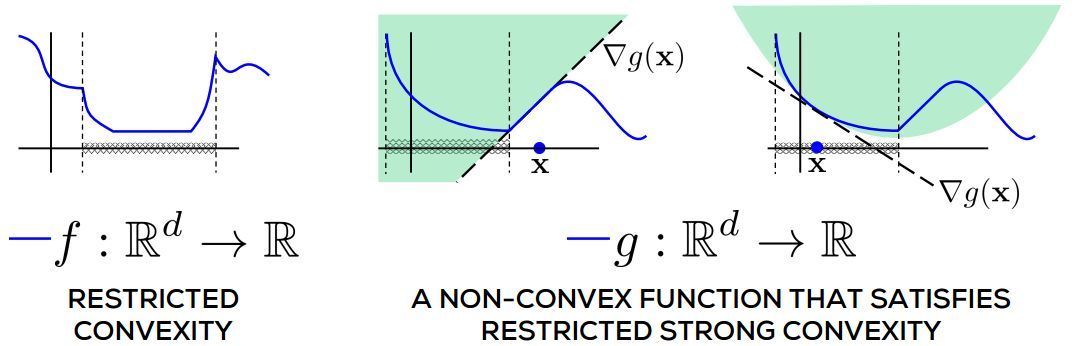
圖 3.1:限制性凸性的描述。f 在整個實線上明顯是非凸的,但在由虛垂直線界定的交叉陰影區域內是凸的。g 是一個非凸函數,滿足限制性的強凸性。交叉陰影區域之外(再次由虛垂直線界定),當其曲線低於切線時,g 甚至不能爲凸,但是在該區域內,它已實際表現出強凸性。
投影梯度下降算法已在算法 1 中陳述。該過程通過採取以梯度爲指導的步驟生成迭代 x_t,以努力減少局部函數值。最後,它返回最後的迭代,平均迭代或者最佳的迭代。

算法 2 概述了用於解決非凸優化問題的廣義投影梯度算法(gPGD)的過程。讀者將會發現這非常類似於算法 1 之中的 PGD。然而,一個關鍵的區別是所做的投影:PGD 利用了凸投影,而 gPGD 利用了非凸投影(如果涉及到一個非凸約束集 C)。

第五章 EM 算法
在本節中,我們會簡述最大期望(Expectation Maximization/EM)的原理。該原理是被人們廣泛使用的學習算法的基礎,如用於學習高斯混合模型,用於學習隱馬爾科夫模型(HMM)的 Baum-Welch 算法,以及混合迴歸。EM 算法是 Lloyd 算法用於 K-均值聚類的一個變體。
儘管 EM 算法在表面上遵循了我們在§5 中研究的交替最小化原則,但由於其在概率學習環境中學習潛變量模型的廣泛適用性,我們認爲深入理解 EM 方法是非常有意義的。爲了讓閱讀體驗自成體系,我們首先會花一些時間在概率學習方法中構建符號。
算法 4 概括了 gAM 對潛在變量學習問題的適應性。注意,算法中的步驟 4 和 6 可以在幾個問題上非常有效地執行。

算法 5 給出了 EM 算法的整體框架。實現 EM 算法需要兩個過程,其一是構造與當前迭代(期望步驟或 E 步驟)對應的 Q 函數,另一個是用於最大化 Q 函數(最大化步驟或 M 步驟)以獲得下一迭代。