
雷鋒網(公衆號:雷鋒網) AI 科技評論按:「Deep Learning」這本書是機器學習領域的重磅書籍,三位作者分別是機器學習界名人、GAN的提出者、谷歌大腦研究科學家 Ian Goodfellow,神經網絡領域創始三位創始人之一的蒙特利爾大學教授 Yoshua Bengio(也是 Ian Goodfellow的老師)、同在蒙特利爾大學的神經網絡與數據挖掘教授 Aaron Courville。只看作者陣容就知道這本書肯定能夠從深度學習的基礎知識和原理一直講到最新的方法,而且在技術的應用方面也有許多具體介紹。這本書面向的對象也不僅是學習相關專業的高校學生,還能夠爲研究人員和業界的技術人員提供穩妥的指導意見、提供解決問題的新鮮思路。
面對着這樣一本內容精彩的好書,不管你有沒有入手開始閱讀,雷鋒網 AI 研習社都希望藉此給大家提供一個共同討論、共同提高的機會。如果大家有看過之前的分享的話,現在除了王奇文之外,我們還繼續邀請到了多位機器學習方面優秀、熱心的分享人蔘與這本書的系列分享。這期邀請到的是陳安寧與大家一起分享他對這本書第四章的讀書感受。
分享人:陳安寧,Jakie,名古屋大學計算力學博士。
「Deep learning」讀書分享(四) —— 第四章 數值計算

大家好,我叫陳安寧,目前在名古屋大學攻讀計算力學博士。今天我要和大家分享的是「Deep Learning」這本書的第四章節,Numerical Calculation,即「數值計算」。
其實大家如果翻過這本書的話,可以看出第四章是整本書所有章節裏面篇幅最少的一章。爲什麼,是因爲其實我們大部分人在運用機器學習或者深度學習的時候是不需要考慮這一章的內容的,這章的內容更多是針對算法的數學分析,包括誤差的增長以及系統的穩定性。

今天分享的主要輪廓包括以下四個點,
第一,在機器學習、包括了深度學習中數值計算的應用。
第二,數值誤差的問題
第三,簡單的分析機器學習系統的穩定性問題
最後,針對優化問題給出了兩種不同的優化算法,一種是梯度下降法,一種是限制優化算法。

我們首先來看一下機器學習中的數值計算問題。所謂的機器學習或者深度學習,其實最終的目標大部分都是極值優化問題,或者是求解線性方程組的問題。這兩個問題無論哪個,我們現在的求解辦法基本上都是基於計算機的反覆迭代更新來求解。因爲目前肯定是沒有解析解的,大家都是通過離散數學來求解這兩個問題。
既然這個過程有迭代或者大量的重複計算,那麼肯定會牽扯到數據的累積。數據累積就極有可能會有誤差的產生。誤差如果過於大或者過於小,在某些特定的情況下都會對系統產生非常致命的影響。
數值誤差的產生原因和避免方法

首先我們來看數值誤差。所謂的數值誤差是指由於計算機系統本身的一些特性產生的誤差,比如說我們知道,無論你使用任何編程語言,它裏面都有很多的數據類型,包括單精度、雙精度、整形、長整型。那麼每一種數據當你定義以後,它在計算機的內存裏面都是有對應的數值範圍和精度範圍的。如果在反覆的迭代計算過程中,你產生的數據超過了數據類型定義的範圍,計算機會自動的進行取捨。
這時就會產生一個問題,因爲取捨就導致了和真實值之間的變化,這個變化就極有可能產生很大的麻煩,如果一個很小的數出現在了分母上,那麼計算機在計算過程中就會得到一個非常大的數,如果這個非常大的數超過了你所定義的數據類型的範圍,計算機就會出現錯誤。
我們可以簡單看一下PPT中這個函數,它叫softmax函數,softmax函數經常會在概率裏面用到。它有很多特性,它的所有元素的softmax之和是等於1的;然後如果所有元素Xi也是相等的話,那麼softmax的每一個元素也是相等的,等於所有n個元素合的1/n。
我們考慮一些比較特殊的情況,比如X是一個非常小的一個量,在指數函數中當這個X非常小的時候,這個指數函數也是非常小,無限趨於零的。無限趨於零的話,假如有限個值相加,比如n=10的話,十個數以後這個分母也是一個非常小的值;如果特別小,比如10-10,這個在計算機裏面一算的話,softmax就會產生一個很大的數,經過多次累積的話,產生的這個大數極有可能超過你的所定義的數據範圍,這個時候你的程序就會報錯。所以我們在計算的時候要避免分母上出現一個極小的數的情況。
同理,分子 xi 如果是一個非常大的數字的話,它的指數也是趨向於無窮的,整個的softmax也是一個非常大的數。這也就是說,分子過大或者是分母過小,都是我們應該在計算過程中極力避免的事情。
舉一個實際應用的例子,爲什麼會有這種過小或過大的情況產生。比如說有一條線,我們要計算某一個點到這個線的距離,這個距離d之後會出現在分母上。對於這樣一個式子,如果這個點我們取得離線過於近的話,這個距離就非常之小,這在實際應用中是經常出現的。這種情況下softmax這個函數就極容易出現問題。
那麼有人會問了,怎麼樣去避免這個問題呢?當然有很多方法,可以的最簡單的辦法就是定義一個max函數,裏面帶有一個常數比如10-4;如果這個距離D很小的話,我們就取這個10-4,限定了d的最小的值就是10-4。
當然這是一個樸素簡單的想法,在實際應用當中,我們可以使用很多其他的方法,比如可以再取一個指數,那麼如果這個值非常小的話,它的整個值就會是趨向於1的,實際上也是一個解決問題的辦法。
這兩個問題,一個叫做分母趨近於0,或者是分子趨近於無窮大,一個叫underflow,下溢,就是指分母過於小;一個是overflow,是指分子過於大,趨近於無窮。這兩個問題都是由於計算機的數據有一個有限的範圍而產生的,並不是我們的算法本身系統產生的。這是Numerical error其中的一種,我們可以把它理解爲,數據類型的範圍限定而導致的對於分子或者分母不能過大或過小而產生的限制。

還有一種極容易出現錯誤的方式,是我們所構造的系統產生的。比如我們在求解線性方程組Ax=B的時候,如果這個矩陣A的是一個病態矩陣,所謂的病態矩陣,最簡單形象的理解就是其中的某些列向量,它們之間的相關性過於大,也就是說列向量非常的接近。
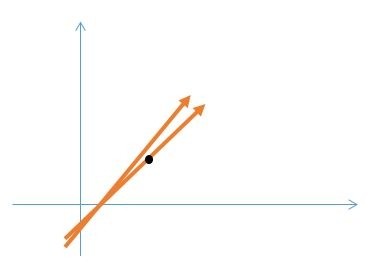
假設這是其中的兩個列向量,取了其中一個列向量上的點。這兩個列向量過於接近的話,對點進行一個微小的變化,它就有可能跑到了另外一個向量上,就是說它的解發生了發生了很大的變化;按理說這個點是屬於向量1的,但僅僅是因爲很小的一個擾動,它就跑到了向量2上,它的解就發生了很大的變化。
有一個一般的辦法判斷矩陣是否病態,就是把矩陣A所有的特徵值λ求出來以後,然後把所有λ裏的最大的值除以最小值,然後取它的模。我們根據這個值可以判斷一個矩陣是否是病態矩陣。
所以很多時候,在進行machine learning或者deep learning之前,我們會對數據進行一個篩選。篩選時候有時候很大的一個目的就是爲了把其中的特徵叫量過於接近的一些數據排除出去,讓我們經過篩選後的矩陣,在它的每一個列向量上有明顯的差異,儘量避免過於接近的列向量的產生。
優化算法的意義以及如何選擇

下面我們來簡單說一下優化算法。絕大部分的機器學習或者說深度學習,都是可以歸結爲一個求極值的最優化問題。最優化問題,我們想到的簡單的辦法當然可以有很多,比如說梯度下降,就是僅僅求一個導數就可以判斷求極值點的方向。
最優化問題,所謂的最優化去找最小值或者是最大值,涉及到兩個問題,一是我怎麼找、往哪個方向走;第二個問題是,我知道了這個方案以後我應該怎麼走,每一步走多少。這基本上是所有求最值的兩個問題,一個是找方向,第二個是找步長。

這是Deep Learning書中關於一些基本函數的定義,包括objective funtion目標函數,或者也可以稱爲損失函數,或者也可以稱爲誤差函數。這時候我們一般都是要求它的最小值,讓誤差或者損失儘量的小。
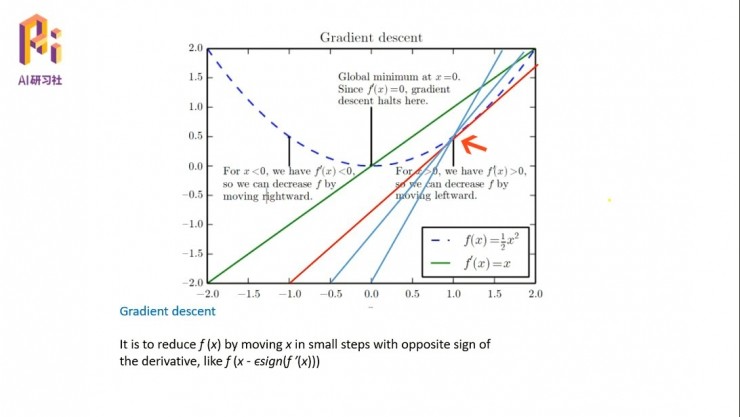
這裏我們看一個非常簡單的例子,怎麼解釋剛纔說的兩個問題,一個是找方向,一個是找步長。這是一個目標函數,一個非常簡單的二次函數。我們看紅色箭頭指的這一點,先看剛纔說的取方向、怎麼走的問題。這裏有無數種方法,每一條直線都可以代表它可以前進的一個方向。但是我們要從中找到一個,因爲這個最低點是我們的目標點,我們要找到從這個點出發到目標點的最快的路徑、一個方向。
這裏面這條紅線是書中原有的,我做了兩條藍色的線。我們從這三條線中可以比較出來,紅線是這三條線裏面朝目標點下降最快的一條線,因爲紅色線在這個點和目標函數的角度是最小的,所以它是過這個點的下降最快的一條線。
然後我們看第二個問題,就是知道了方向以後怎麼去走。對於每一個步長,我們在這裏面引入一個ε的權值,爲了保持系統的穩定性,一般會取一個比較小的值,比如說0.001或者是10-4這樣的一個小值,讓這個點緩慢地沿着這個紅色的這個方向,一小步一小步地,朝着目標函數前進。
但是這裏面會有一些問題,比如說我們會遇到一些特殊的點。剛纔的比較簡單的二次函數是沒有問題的,但是看一下後面一些複雜的函數。
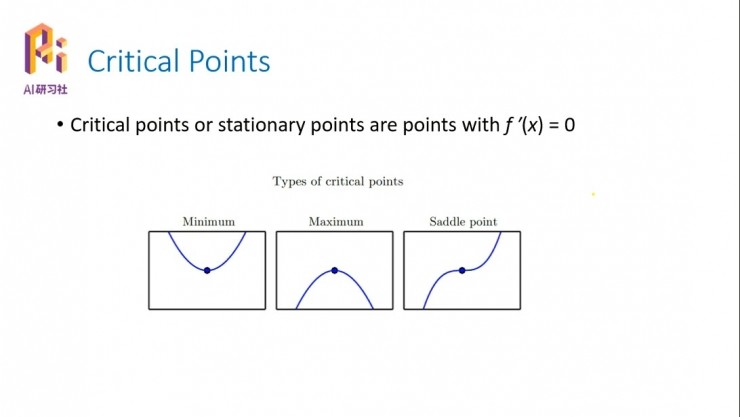
這裏是一些特殊的點,critical points,我們可以把它稱爲臨界點。
所謂的臨界點是指,它的一次導數爲零,也就是說這個點往左或者往右都會都會變大或變小,這個點本身就是這個小的局部系統裏面的一個極值點。如果你往兩邊走都是變大,那麼它就是一個極小值點;如果你往兩邊走都是變小,那麼它就是一個極大值點;如果一邊減小、一邊變大,這種情況是我們在計算裏面最不想看到的情況,叫做駐點,雖然它的導數也是零,但是這個點並不是我們所期待的那個objective point,不是我們想要找的目標點。
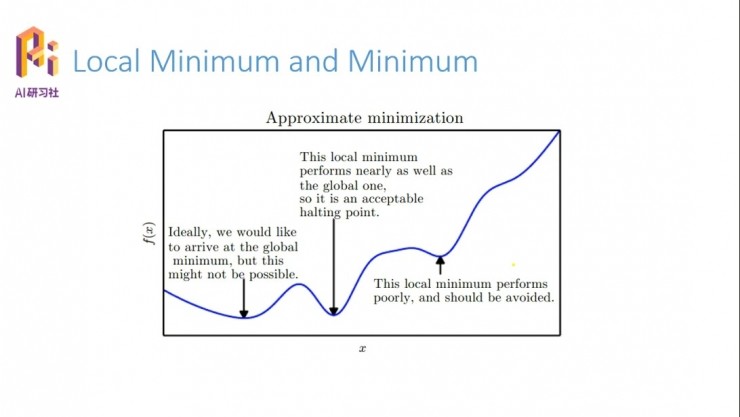
我們看一個複雜一點的。像這個函數曲線,圖中有三個點都滿足我們剛纔說的一階導數爲零,但是右側這兩個點就不是我們想要的,最左側點的值更小。這個時候就有兩個問題,就是局部極值和全局最值的問題。這三個點都可以稱爲局部的極值點,只要滿足一階導數爲零,但是怎麼判斷你所求的局部極值點是否是全局的最值點?有一個簡單的辦法是把整個系統所有的極值點都找到,然後比從裏面比較出最小值;但是在實際應用中是不會這麼做的,一是浪費太多的計算資源,二是因爲起點的不同,找這個局部極值點也會有很多的問題。
所以如果要是把每一個極值點都找的話,會非常的繁瑣,會浪費大量的資源。那麼,我們設計的系統怎麼樣保證找到的這個點是一個最優點、或者說是全局的最值點呢?

之前介紹的都是隻有單個變量的系統,現在看一下有多個變量的系統。在單變量系統裏面,我們只需要求一個輸入的導數;但是在多變量的系統裏面,有很多的輸入,就有一個偏導數的概念,假定其它的變量固定、系統對其中的某一個變量求導的話,就稱之爲關於這個變量的偏導數。

把所有的變量的偏導數求出來,並用向量的形式表示出來,可以表示成這個形式。剛纔我們分析過了,如果要找到局部極值點的話,我們最快的方向是求導數、沿着梯度的方向;那麼多變量系統裏面也一樣,就是說我們要求一個系統的最小值的話,還是通過求導,但這次是多變量的系統,所以我們的求導要改成偏導數向量的方向來去尋找新的最值。

這種梯度下降算法在實現的時候會有一些不同,比如根據每次下降所採用的系統點數的不同,可以大致分爲兩大類,一種叫做Batch Gradient Desecent,就是批梯度下降。所謂的「批」就是批量,比如說我們現在有一個系統h(x)等於θi*xi的合集(右上角),這是一個非常簡單的線性系統。按照我們之前所說的,首先要求出這個系統的目標函數,我們這裏用了一個最小二乘法的目標函數,然後求這個目標函數的最小值問題。
首先我們要求它的偏導數,∂J(θ)/∂θj,它表示一個方向,然後沿着這個方向更新那個變量。在變量更新的時候,批梯度下降是指每一次的變量更新,都會用到所有的xj;然後從i=1到m,會用到所有的單獨變量的偏導數。比如假設這個系統裏面的每一個樣本有五個特徵的話,那麼在更新任意一個權值的時候都要把這五個特徵遍歷一遍。
這樣的話,如果是一個非常小的系統,比如說樣本數量不是很多、每一個樣本所包含的特徵也不是很多的話,這個是完全可以的,因爲它求解的是一個全局的最優,考慮了考慮到了每一個變量方向的梯度問題,所以求的是全局的最優下降的方向。但是所求的系統往往有大量的樣本,同時每一個樣本還包含了不少的特徵,簡單分析一下這個系統的計算量的話,假設它的樣本數量是n,然後每一個的特徵是m,那麼其中一個樣本的計算量是m×m;有n個樣本的話,總的計算量是m×m×n。如果樣本1萬、2萬、10萬超級大的話,每一次迭代的計算量是非常大的。
這個時候大家就想到另外一種辦法,我能不能在每一次更新權值的時候,不用到所有的特徵,只用其中的所求變量的特徵,這就是我們所謂的隨機梯度下降Stochastic Gradient Descent。隨機梯度就是說,每一次針對權值的更新,只隨機取其中的一個i,就是隨機取其中的一個特徵來計算。這樣它的計算量立馬就下降了,同樣是n個樣本就變成了m×n。因爲原來的公式裏面有一個求和符號,需要求m個特徵的值;這裏面每次只求一個特徵的。所以這個計算量就少了非常多。
這又引發了一個問題,通過剛纔分析,我們知道BGD是全局自由梯度下降,SGD是隨機梯度現象,隨機梯度中只找了其中一個變量所在的方向進行搜索,向目標點前進,那麼這種方法是否能保證最後到達目標呢?理論上是有證明的,是可以的,只是這個會收斂的非常慢。

這兩個方法就有點矛盾,一個是計算量大,但是全局最優,收斂比較快;一個是計算量小,但是收斂比較慢,只能找到最優目標值的附近。所以又產生了一種調和的算法,叫做小批量梯度下降,Mini-Batch Gradient Descent。其實很簡單,既不像批量用到所有的特徵去更新權值,也不像隨機梯度下降只用其中一個,我選取一部分,假設每個樣本有100個特徵,我只取其中的10個特徵用於每一次的權值更新。那麼首先它的計算量是下降的,其次它也並不是僅僅按照其中某一個、而是它是按照了10個特徵向量所在的方向進行搜索,既保證了搜索速度,又保證了計算量,這是目前在梯度下降中用的比較多的一個方法,算是一個BGD和SGD兩種方法的折中方法。

它們三者的優缺點分別就是,批量是計算量大,隨機是計算量小,但是搜索精度有一定的問題;Mini-batch就是權衡了兩者。
剛纔所有的分析都是基於一階導數,這也是在簡單的線性系統優化中常用的。其實二階導數對於系統的分析也是非常有用的。
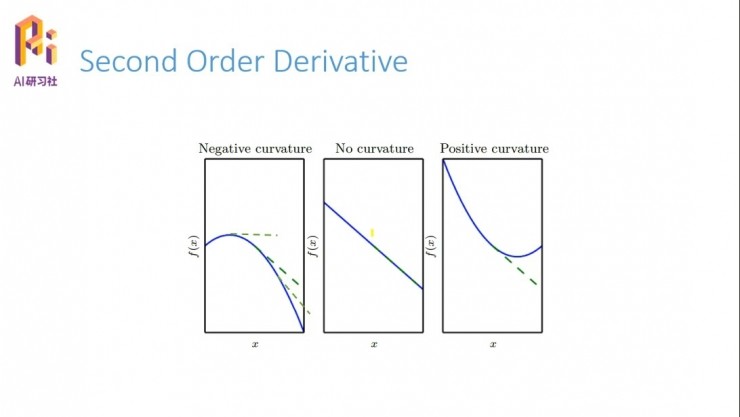
看一下這幾個簡單的例子。我們知道一階導數的意義表示的是f(x)的變化,二階導數的意義就是一階導數的變化情況。比如說第一幅圖,它的一階導數從正(上升)到0(水平)再到負的(下降),不停地減小,就可以知道它的二階導數是小於0的。第二幅圖一條直線的話,它的斜率也就是一階導數是永遠不變,那麼它的二階導數就永遠是0;同理第三個圖指的是二階導數大於零的情況。

二階導數的意義就是我們可以分析這個系統。下面先介紹一個雅克比矩陣(Jacobian Matrix),我們的系統是一個多輸入、多輸出的系統,它變量的範圍是Rm 域的範圍,輸出是Rn 域的範圍,那麼f(x) 的雅克比矩陣就是,針對所有的輸入啊求導,比如第一行是那個f1對所有的輸入變量求導,第二行就是f2,f的第二個變量,對所有的變量求導;同理,最後一行就是fm對所有的變量求導。這就是雅克比矩陣的定義。
雅克比矩陣是一階的求導矩陣,還有二階求導矩陣黑塞矩陣(Hessian Matrix)。

黑塞矩陣的定義其實也很簡單,每一個f(x) 同時對兩個方向的變量求二次導數。當然你也可以把它看成雅克比矩陣的變形,黑塞矩陣裏的每一項相當於雅克比矩陣裏面的每一項再求導,因爲二階導數可以看成一次求導再求導。這是黑塞矩陣的定義。
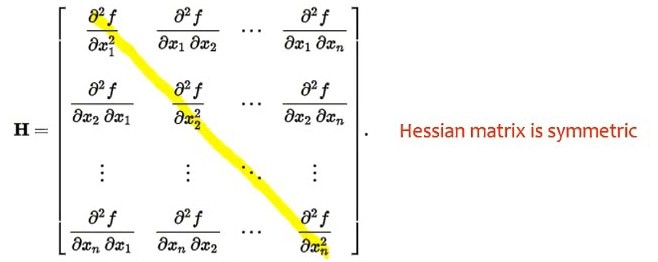
黑塞矩陣有一個特點,對於一個系統,如果它的偏導數不分方向的,就是說先對xi求導、或者先對xj求導,求導的先後順序不影響二次導數值的話,那麼黑塞矩陣就明顯是一個對稱矩陣,因爲xi、xj可以互相交換。就是說對先對x2求導或者先對x1求導是沒有關係的,那麼∂x1*∂x2和∂x2*∂x1是相等的。

那麼二階矩陣有什麼影響,它對先前的一階矩陣梯度下降的不足有什麼樣的改進呢?簡單分析一下,一個f(x) 可以做這樣的泰勒展開,其中包含特定點的值,這個g 表示的是一階導數,也就是梯度,然後H是一個二階的梯度矩陣。
當我們更新x值的時候,比如說現在是x0,然後下一步更新到x0-εg的時候(這是剛纔梯度下降的定義嘛),帶入這個泰勒展開會得到圖中下方的公式。
列出這個公式的主要目的是爲了考察梯度下降的步長係數應該怎麼取值比較好。剛纔講過了,剛開始我們可以隨便給一個比較小的值,0.01、0.004或者更小的值。但是實際的情況下,我們不想隨機給一個,而是通過數學的分析得到一個比較好的值,從而定義這個步長係數,可以走得既快又準確。
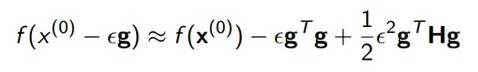
帶入得到這個公式之後(當然這時候我們可以把約等號當作等號),我們可以把它當做一個關於ε的函數,其它的變量可以都當作常數。如果要得ε的一個比較優化的值的話,我們可以看作f(ε) 等於這個式子,然後對它關於ε求導,最後在所有可能的係數裏面得到一個比較好的係數。有了這個係數就可以保證我們的步長取得又大又穩。

下面我介紹兩個方法,一個是僅僅用了一階導數的、我們前面提到的gradient descent;另一個是牛頓方法,這是用到二階導數的方法。梯度下降僅僅用到了一階導數,所以我們把它稱爲一階優化算法;牛頓方法用到了二階,我們就把牛頓方法稱爲二階優化算法。

我們看一下牛頓迭代方法,這是剛纔提到的泰勒展開,然後現在想要找到這個系統的極值點,當然,僅僅求導就行了。根據一階導數爲0,它的臨界點就是圖中下方這個公式。這樣我們更新就按照這個公式。
這個公式有什麼意義呢?就是一次直接找到了這個critical point,過程中用到的是黑塞矩陣。因爲在這裏面用到了黑塞矩陣,所以我們把牛頓方法稱爲一個二階方法。

這之前,我們遇到的所有求極值的問題都是就是無約束的,就是freestyle,x沒有任何的約束。僅僅是求目標函數的最小值問題。但是實際情況裏有大量的約束問題,這就牽扯到了另外的約束優化的問題。
這是維基百科上關於約束優化的定義。
首先f(x) 是目標函數,如果沒有下面這一堆subject to的話,它就是我們之前講到的最優化問題,你可以用梯度下降,也可以用牛頓法來求解。但是這個時候它有了很多的約束,比如x必須滿足某一個函數,xi代進去要等於一個特定的值ci。這是一個等式,所以又把它稱作等式約束;相反就是不等式約束問題。
遇到這樣問題應該怎麼做?很容易想到能不能把這兩個約束的條件整合到目標函數裏面,然後對這個整合的系統再求優化問題。其實我們做工程很多時候都是這樣的,之前先有一個基本的、best的處理方法,再遇到一個問題以後,就想辦法把新產生的問題去往已知的基本問題上靠攏。
這裏介紹一個KKT的約束優化算法。KKT優化算法其實很簡單,它就是構造了一個廣義的拉格朗日函數,然後我們針對這個廣義的拉格朗日函數,或者是這個系統來求它的極值。
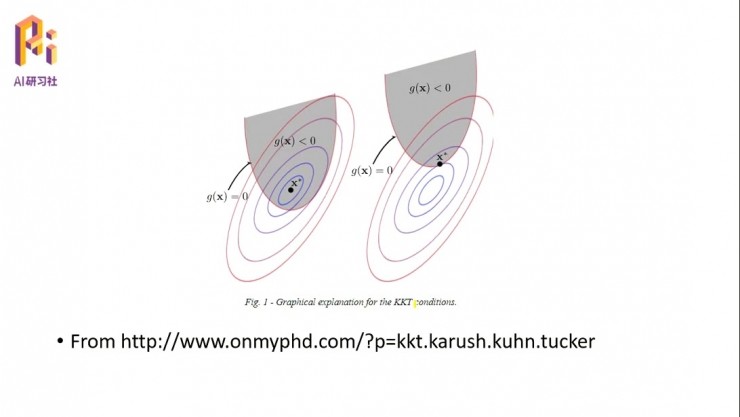
我們可以從圖片上來看這個約束問題。比如我們選了一個初始點,如果沒有陰影部分的面積,那就從初始點隨便怎麼走去找這個最優的x。走的方法就是它的梯度方向。但是現在有約束問題的話,x的取值必須要在陰影範圍之內走動,這是一個比較形象的約束問題的表徵。

前面提到我們要構造拉格朗日函數。要構造拉格朗日函數也簡單,我們現在有一個等式約束,還有一個不等式約束,只要在等式約束和不能約束之前加入一個係數,當然我們是把這些係數看作變量的。把這些係數加入到原來的函數之上,構成了一個新的函數系統,我們就可以把它叫做廣義拉格朗日函數。
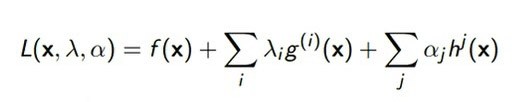
之前我們是僅僅是求f(x) 的最小值,現在加入了這兩個,我們可以根據它的特徵分析一下。
首先,h(x) 小於等於0的話,針對它的係數α,我們就要求它的最大值;然後看 λ,因爲 λ 是一個常數,求最大或者最小是一樣的;最後又歸結到f(x),還是求它的最小值。當然,我們也可以兩個累加前面都變成負號,那麼同理下面可以變成要求它的最小值。
其實也可以很好理解,就是說原來是一個f(x),現在加入了一個東西,這個東西滿足的條件是對於任意的x,h(x)都必須是小於等於0的。那麼如果我的最大值都小於等於0的話,那肯定所有值都小於等於0了。所以我這邊要求一個最小值。
當然我假設加入的這部分是正的,這邊所有的α都是大於零的,那麼L(x,λ,α) 裏αjhj(x) 就始終是小於等於0的;小於等於0的話,我只要讓它的最大值滿足的小於等於0,那麼它所有的其他值肯定也是滿足這個條件的。這就是如何構建一個拉格朗日函數的方法。
有了這個構建的函數以後,它的極值問題就可以用梯度下降的方法來求解。

我們舉一個簡單的例子,最簡單的,線性最小二乘法,這個是在求誤差的時候最常用的損失函數或者目標函數了。那麼我們可以用到前面講到的梯度下降法,求它的導數,然後x更新的話就是用一個小的補償係數乘以Δx,就是它的梯度。當然你也可以用牛頓方法,用求它的二階導數來更新。

現在我們把這個系統稍微改一下,把它變成一個受限的系統。比如我們要求向量x滿足這個條件,這樣它就變成了一個帶有限制的優化問題。這個時候我們可以構造拉格朗日函數,原函數不變,加上它的限制條件,前面加上一個λ變量,然後就可以寫出它的目標函數。
首先f(x) 是不變的,然後因爲xTx小於等於1,所以這邊要求最大的(當然如果xTx大於等於1,你這邊要求最小的)。然後怎麼更新這個系統呢,x可以這樣來表示
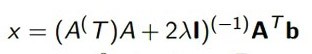
基本上就是求逆的操作。λ滿足的一個梯度條件是,把它看作單變量,對它求導,它的導數需要滿足
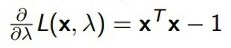
這樣Deep Learning書的第四章書基本上就講完了。
總結
最後簡單總結一下,這一章主要講的問題。
第一,我們在做數值計算,包括深度學習或者機器學習的時候,我們要注意裏面的變量,尤其是在分母上的變量,不要出於出現過小的值,比如距離,分母不要過橋,分子不要過大。現在是有軟件是可以幫助我們檢測的,但是因爲我們平時用到的算法基本上是成熟的,或者是用了很多Library/庫,其中已經對一些異常狀況做過提前預防,所以我們的計算中是不存在這個問題的。一般是針對我們要自己動手設計出新的計算方法時纔會考慮這個問題;平時的計算過程中一般不需要考慮系統的穩定性問題的。你如果設計一個新的系統,你就要分析一下這個系統的穩定性。
然後就是梯度下降的意義,就是我們找了一個什麼樣的方向去接近目標函數,有了方案以後我們應該怎麼走,每一步應該走多少;有時候你走的過大的話,也會導致系統的發散。
其實在這本書的最後作者也說了,目前Deep Learning系統缺少嚴格的理論保障。爲什麼我們做機器學習的時候經常說調參數、調參數,就是因爲很多東西可以說是試出來的,並沒有嚴格的數學證明說某一個值應該怎麼取。這一章節在最後也說了一個目前使用的深度學習算法的缺點,就是因爲它的系統目前過於複雜,比如一層接一層的函數的疊加或者是相乘,它的系統分析就會很複雜,很難有一個明確的理論去分析這個系統的各種特徵。如果僅僅是一個簡單的f(x)=x2,這種系統無論怎麼做都行,它已經被分析的太徹底了,無論怎麼算都會有一個精確的算法在那裏。所以前面講的誤差也僅僅是在一個常見的容易出錯的地方給了一個比較好的指導,但實際的計算過程中還會遇到各種各樣的問題。這個時候一是要靠經驗,二是也希望會有越來越多的數學理論來支持深度學習的系統分析。
還有就是,我們在做計算的時候都知道有一個天然的矛盾,就是計算量和精度的問題。計算量大就會讓精度提高,但是有時候過大的計算量又是我們承受不了的,所以這也是一個矛盾。現在的很多算法其實也就是在中和這個矛盾,既要降低計算量,要保持我們能夠接受的精度。所以現在有很多前處理的方式,針對大量的數據要怎麼樣處理,讓設計的系統最後既能夠滿足我們的要求,又儘量的減少計算量,同時也儘量避免一些不必要的誤差。其實這是就是一個洗數據的過程,把數據洗得乾淨一點,把噪音和沒有用的數據都淘汰掉的過程。
今天就和大家分享到這裏,如果有什麼問題的話,歡迎大家在羣裏面討論。
機器學習的數學數學理論其實比較匱乏,所以有很多值得討論的問題,包括其實有我剛纔有好幾個點想講沒有講的,因爲時間有限,比如說二階的優化問題,怎麼樣去用二階的優化問題去保證一階優化找到那個全局的最小點,而不是局部的最小點。其實這個在多目標、多變量的系統裏面,目前還沒有特別好的方法,當然在單系統裏面就不存在這個問題,有很多方法去解決。今天就先到這裏,謝謝大家。
(完)
雷鋒網 AI 科技評論整理,感謝陳安寧此次分享,後續更多章節的分享請大家繼續關注我們!
相關文章:
「Deep Learning」讀書系列分享第二章:線性代數 | 分享總結
「Deep Learning」讀書系列分享第三章:概率和信息論 | 分享總結
