作者:René Vidal、Joan Bruna、Raja Giryes、Stefano Soatto
近年來,深度學習大獲成功,尤其是卷積神經網絡(CNN)在圖像識別任務上的突出表現。然而,由於黑箱的存在,這種成功一度讓機器學習理論學家頗感不解。本文的目的正是要揭示深度學習成功的奧祕。通過圍繞着深度學習的三個核心要素——架構、正則化技術和優化算法,並回顧近期研究,作者爲深層網絡的若干屬性,如全局最優性、幾何穩定性、學習表徵不變性,提供了一個數學證明。
論文:Mathematics of Deep Learning

論文鏈接:https://arxiv.org/abs/1712.04741
摘要:近期深度架構用於表徵學習和分類之後,識別系統的性能獲得了巨大提升。然而,這一成功的數學原因依然不得而知。本文將回顧近期研究,爲深層網絡的若干屬性,如全局最優性、幾何穩定性、學習表徵不變性,提供一個數學證明。
1. 引言
深層網絡 [1] 是在輸入數據上執行序列操作的參數模型。通俗講,每個這樣的操作被稱爲「層」,每個層包括一個線性變換(比如其輸入的卷積)和一個逐點非線性「激活函數」(比如 Sigmoid)。近期在語音、自然語言處理、計算機視覺的不同應用中,深層網絡實現了分類性能的巨大提升。深層網絡取得成功的關鍵原因是其較於傳統神經網絡有着大量的層;但也有其他架構調整,比如 ReLU [2] 和殘差「捷徑」連接(residual shortcut connections)[3]。成功的其他主要因素還包括海量數據集的可用性,比如 ImageNet 等數據集中的數百萬張圖像,以及用於解決由此產生的高維優化問題的高效 GPU 計算硬件(可能具備高達 1 億個參數)。
深度學習的成功,尤其是 CNN 在圖像任務上的成功,給理論學家帶來了很多困惑。如果我們打算揭開其成功的奧祕,那麼深度學習的三個核心因素——架構、正則化技術和優化算法,對訓練優秀性能的深層網絡、理解其必然性和互動尤其關鍵。
A. 近似值、深度、寬度、不變性
神經網絡架構設計的一個重要屬性是可以近似輸入的任意函數。但是這個能力如何依賴於架構的參數,比如其深度和寬度?早期研究表明,具有單一隱藏層和 Sigmoid 激活函數的神經網絡是通用函數近似器 [5] [6] [7] [8]。但是,寬的淺層網絡的容量可被深層網絡複製,且性能出現顯著提升。一個可能的解釋是深層架構相較於淺層架構可以更好地捕獲數據的不變性。比如在計算機視覺中,物體的類別不會隨着視角、照明等的變化而變化。對於爲什麼深層網絡能夠捕獲此類不變性的數學分析仍然不得而知,但近期進展已經爲深層網絡的特定子類別提供了一些解釋。特別是,散射網絡 [9] 是一種深層網絡,其卷積濾波器組由複雜的多分辨率小波族羣給出。正由於這種額外結構,它們被證明是穩定和局部不變的信號表徵,並揭示了幾何和穩定性的基本作用,這是現代深度卷積網絡架構泛化性能的基礎(詳見第四章)。
B. 泛化和正則化
神經網絡架構的另一個重要屬性是可以利用少量訓練樣本進行泛化。統計學習理論的傳統結果 [10] 表明,實現良好泛化所需的訓練樣本數隨網絡大小呈現多項式增長。然而,在實踐中,深層網絡訓練所需的參數數量要遠大於數據量(N D regime),而使用非常簡單的(看似相反)正則化技術可以防止過擬合,如 Dropout 在每次迭代中通過簡單凍結參數的隨機子集即可防止過擬合。
一個可能的解釋是,更深層的架構產生輸入數據的嵌入,近似地保留同一類中數據點之間的距離,同時增加類別之間的分離。本文將概述 [12] 的近期研究工作,它使用壓縮感知和字典學習工具證明具有隨機高斯權重的深層網絡可以執行保留數據點距離的嵌入,其中相似輸入可能具有相似輸出。這些結果有助於理解網絡的度量學習屬性,並引出由輸入數據的結構決定的泛化誤差的範圍。
C. 信息論屬性
網絡架構的另一個關鍵屬性是產生良好「數據表徵」的能力。簡單說,表徵是對一個任務有用的輸入數據的任意函數。比如,最佳表徵是由信息論、複雜性或不變性標準 [13] 量化出的「最有用」的一個表徵。這類似於系統的「狀態」,智能體將其存儲在內存中以代替數據來預測未來的觀察結果。例如,卡爾曼濾波器的狀態是用於預測由具有高斯噪聲的線性動態系統生成數據的最佳表徵;即用於預測的最小充分統計量。對於數據可能被不包含任務信息的「麻煩」所破壞的複雜任務,人們也可能希望這種表徵對這種麻煩具有「不變性」,以免影響未來的預測。通常來說,任務的最佳表徵可被定義爲最小充分統計量,並且對影響未來(「測試」)數據的各種變化保持不變性 [14]。儘管研究者對錶徵學習有着強烈興趣,但是解釋深層網絡作爲構建最優表徵的性能的綜合理論尚不存在。事實上,即使是充分性和不變性這樣的基本概念也得到了不同的對待 [9] [14] [15]。
近期研究 [16]、[17]、[18] 已經開始爲深層網絡學習的表徵建立信息論基礎,包括觀察到信息瓶頸損失 [13](它定義了最小充分性的寬鬆概念)可被用於計算最佳表徵。信息瓶頸損失可重寫爲交叉熵項的總和,這正是深度學習中最常用的損失,帶有一個額外的正則化項。後者可通過在學習表徵中引入類似自適應 dropout 噪聲的噪聲來實現 [17]。由此產生的正則化形式在 [17] 中被稱爲信息 dropout,表明在資源受限的條件下學習可以得到改善,並可導致「最大分離式」表徵(「maximally disentangled」representation),即表徵的組成部分之間的(總)相關性是最小的,使得數據具有獨立特徵的特徵指標。此外,類似技術表明針對對抗擾動的魯棒性有所改善 [18]。因此,研究者期望信息論在形式化和分析深層表徵的屬性以及提出新型正則化項方面起到關鍵作用。
D. 優化
訓練神經網絡的經典方法是使用反向傳播最小化(正則化)損失 [19],它是一種專門用於神經網絡的梯度下降方法。反向傳播的現代版本依靠隨機梯度下降(SGD)來高效近似海量數據集的梯度。雖然 SGD 僅用於嚴格分析凸損失函數 [20],但在深度學習中,損失函數是網絡參數的非凸函數,因此無法保證 SGD 能夠找到全局最小值。
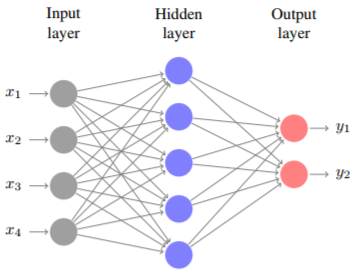
圖 1:神經網絡圖示,其中 D = d_1 = 4 個輸入,d_2 = 5 個隱藏層,C = d_3 = 2 個輸出。輸出可寫爲 y = (y_1, y_2) = ψ_2(ψ_1(xW^1 )W^2 ),其中 x = (x_1, . . . , x_4) 是輸入,W^1 ∈ R^4×5 是從輸入層到隱藏層的權重矩陣,W^2 ∈ R^5×2 是從隱藏層到輸出層的權重矩陣,ψ_1 和 ψ_2 是激活函數。
實踐中有大量證據表明 SGD 爲深層網絡提供良好的解決方案。最近關於理解訓練質量的研究認爲,臨界點更可能是鞍點而不是假的局部極小值 [21],局部極小值集中在全局最優值附近 [22]。近期研究還揭示了 SGD 發現的局部極小值帶來參數空間非常平坦區域的良好泛化誤差 [23]。這激勵了 Entropy-SGD 等專用於尋找此類區域的算法,並從統計物理學中的二進制感知機分析中得出相似的結果 [24]。它們已被證明在深層網絡上表現良好 [25]。令人驚訝的是,這些統計物理學技術與偏微分方程(PDE)的正則化屬性密切相關 [26]。例如,局部熵——Entropy-SGD 最小化的損失,是 HamiltonJacobi-Bellman 偏微分方程的解,因此可寫成一個懲罰貪婪梯度下降的隨機最優控制問題。這個方向進一步導致具備良好經驗性能的 SGD 變體和凸優化標準方法(如 infconvolutions 和近端方法(proximal methods)。研究人員現在纔剛剛開始從拓撲方面闡釋深層網絡的損失函數,拓撲決定了優化的複雜性,而它們的幾何結構似乎與分類器的泛化屬性有關 [27] [28] [29]。
本文將概述近期的研究論文,展示深度學習等高維非凸優化問題的誤差曲面具有一些良性屬性。例如,[30]、[31] 的工作表明,對於某些類型的神經網絡,其損失函數和正則化項都是相同程度的正齊次函數的和,多個分量爲零或逼近爲零的局部最優解也將是或逼近全局最優解。這些結果也將爲正齊次函數 RELU 的成功提供一個可能的解釋。除了深度學習,這個框架的特殊情況還包括矩陣分解和張量分解 [32]。
E. 論文大綱
本論文的其餘部分安排如下。第二章介紹深層網絡的輸入輸出圖。第三章研究深層網絡的訓練問題,併爲全局最優性建立條件。第四章研究散射網絡的不變性和穩定性。第五章研究深層網絡的結構屬性,如嵌入的度量屬性以及泛化誤差的界限。第六章研究深度表徵的信息論屬性。
2. 預備工作
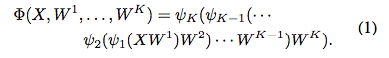
3. 深度學習中的全局最優性
本章研究從 N 個訓練樣本 (X, Y ) 中學習深層網絡的參數。在分類設置中,X ∈ R^N×D 的每一行代表 R^D 中的一個數據點,Y ∈ {0, 1} ^ N×C 的每一行代表每個數據點與 C 類別的從屬關係,即如果 X 的第 j 行屬於類 c ∈ {1, . . . , C},則 Y_jc = 1,反之,則 Y_jc = 0。在迴歸設置中,Y ∈ R^N×C 代表 X 行的因變量(dependent variable)。學習網絡權重 W 的問題可以表述爲以下優化問題:
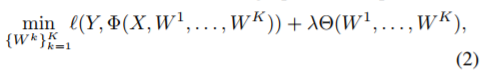
其中是損失函數,用於評估真正輸出 Y 和預測輸出 Φ(X, W)(公式 (1))之間的一致程度;Θ 是正則化函數,用於防止過擬合,如通過正則化執行的權重衰減;λ>0 是平衡參數。
A. 神經網絡訓練的非凸挑戰
神經網絡訓練的重要挑戰是(2)中的優化問題是非凸的,即使損失函數通常是 Φ 的凸函數,如平方損失;Φ(X, W) 通常是 W 的非凸函數,因其是(1)中 W_k 變量和非線性函數 ψ_k 的積。這對現有優化算法來說是一個巨大的挑戰,如梯度下降、隨機梯度下降、交替最小化、塊座標下降、反向傳播、擬牛頓法等,這些優化算法通常只能確保收斂至目標函數的臨界點 [33] [34] [35] [36]。
但是,對於非凸問題,臨界點集不僅包括全局最小值,還包括局部極小值、局部極大值、鞍點和鞍點 plateaus,如圖 2 所示。因此,非凸問題使該模型呈現一定的不適定性,因其不僅是重要的模型公式也是實現細節,如模型如何初始化以及優化算法的細節,這對模型性能產生很大影響。

圖 2. 非凸函數的臨界點示例(紅色)。(a,c) plateaus;(b,d) 全局最小值;(e,g) 局部極大值;(f,h) 局部極小值。
B. 使用單個隱藏層的神經網絡最優性
關於神經網絡全局最優性的早期研究 [41] 展示了:使用線性激活函數和單個隱藏層的網絡的平方損失有一個全局最小值,其他臨界點均爲鞍點。但是,[42] 中的網絡示例證明,當激活函數非線性時,即使使用可分數據,網絡中的反向傳播算法 [19] 依然失敗了。不過,這些網絡示例不通用,[43]、[44] 展示了使用線性可分數據時,反向傳播通常可以找到全局最小點。
C. 使用隨機輸入和權重的神經網絡最優性
近期多個研究利用隨機矩陣理論和統計物理學工具分析了多層神經網絡的誤差曲面。例如,[21] 的作者認爲,在特定假設條件下,高維優化問題的臨界點更有可能是鞍點而非局部極小點。
D. 正齊次性網絡(positively homogeneous network)的全局最優性
近期研究 [30]、[31] 很大程度上沿用了上述論文的想法,但是使用的方法存在顯著區別。具體來說,[30]、[31] 利用純粹確定性方法分析了(2)中的優化問題,該方法不對輸入數據分佈、網絡權重參數數據或網絡初始化做任何假設。[30]、[31] 使用該方法證明只有鞍點和 plateaus 纔是我們需要關心的臨界點,因爲對於足夠規模的網絡,不存在需要攀爬目標曲面再擺脫局部極小值(如圖 2 中的 (f)、(h))。
4. 深度學習中的幾何穩定性
理解深度學習模型的重要問題是從數學角度定義其歸納偏置(inductive bias),即定義迴歸/分類任務的類別,這樣它們可以實現優秀的性能,或至少比傳統方法要好。
在計算機視覺任務中,卷積架構爲最成功的深度學習視覺模型提供基礎的歸納偏置。幾何穩定性有助於我們理解其成功。
5. 深度學習基於結構的理論
A. 神經網絡中的數據結構
理解深度學習的一個重要方面就是理解數據結構和深層網絡之間的關係。對於正式分析來說,假設一個網絡具備隨機獨立同分布高斯權重,這是深層網絡訓練中的常見初始化設置。近期研究 [56] 顯示此類具備隨機權重的網絡將數據的度量結構沿層傳播,實現網絡計算特徵的原始數據的穩定恢復,該特性經常會在一般深層網絡中遇到 [57] [58]。
B. 泛化誤差
上文說明數據結構和訓練過程中獲取的網絡誤差之間存在關係,這引發對深層網絡的泛化誤差與數據結構之間關係的研究。泛化誤差——經驗誤差和期望誤差之差,是統計學習理論中的基礎概念。泛化誤差有可能爲利用訓練樣本學習的原因提供見解。
補充:
http://www.vision.jhu.edu/tutorials/ICCV15-Tutorial-Math-Deep-Learning-Intro-Rene-Joan.pdf