前言
基本的神經網絡的知識(一般化模型、前向計算、反向傳播及其本質、激活函數等)小夕已經介紹完畢,本文先講一下深度前饋網絡的BP過程,再基於此來重點講解在前饋網絡中用來初始化model參數的Xavier方法的原理。
前向
前向過程很簡單,每一層與下一層的連接邊(即參數)構成了一個矩陣(即線性映射),每一層的神經元構成一個激活函數陣列(即非線性映射),信號便從輸入層開始反覆的重複這兩個過程直到輸出層,也就是已經在《神經網絡激活函數》中詳細講過的線性與非線性交替映射的過程:
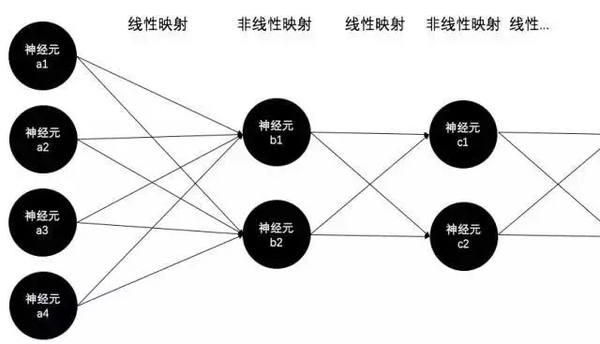
反向
誤差反向傳播的過程也很簡單,其本質就是基於鏈式求導+梯度下降,原因已在《BP算法的本質》中講解,這裏就重點講解一下BP算法的過程。
首先往上翻一翻,記住之前說過的前饋網絡無非就是反覆的線性與非線性映射。然後:
首先,假設某個神經元的輸入爲z,經過激活函數f1(·)得到輸出a。即函數值a=f1(z)。如果這裏的輸入z又是另一個函數f2的輸出的話(當然啦,這裏的f2就是線性映射函數,也就是連接某兩層的權重矩陣),即z=f2(x),那麼如果基於a來對z中的變量x求導的時候,由於
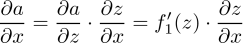
顯然只要乘以激活函數f1的導數,就不用操心激活函數的輸出以及更後面的事兒了(這裏的「後面」指的是神經網絡的輸出端方向),只需要將精力集中在前面的東西,即只需要關注z以及z之前的那些變量和函數就可以了。因此,誤差反向傳播到某非線性映射層的輸出時,只需要乘上該非線性映射函數在z點的導數就算跨過這一層啦。
而由於f2(·)是個線性映射函數,即 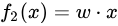 ,因此
,因此
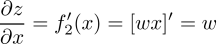
因此,當誤差反向傳播到線性映射層的輸出時,若想跨過該層,只需要乘以線性映射函數的參數就可以啦~即乘上w。
而這裏的x,又是更前面的非線性映射層的輸出,因此誤差在深度前饋網絡中反向傳播時,無非就是反覆的跨過非線性層和線性層,也就是反覆的乘以非線性函數的導數(即激活函數的導數)和線性函數的導數(即神經網絡的參數/權重/連接邊)。
也就是下面這張圖啦(從右往左看):
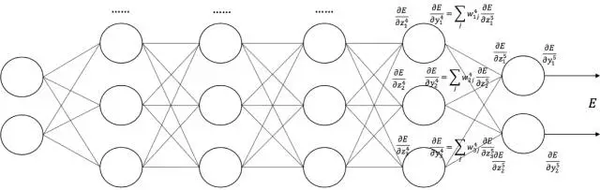
(圖片來自中科院自動化所趙軍老師的課件)
Xavier
前向與反向都講解完了,下面就是更加實用的工程tricks。提起tricks,先想到參數的初始化啦。如果無腦的將model的參數初始化成全0,那訓練到天荒地老也是個廢貓倒了。
而爲什麼初始化成全0就不行了呢?這個不用講啦,全0的時候每個神經元的輸入和輸出沒有任何的差異,換句話說,根據前面BP算法的講解,這樣會導致誤差根本無法從後一層往前傳(乘以全0的w後誤差就沒了),這樣的model當然沒有任何意義。
那麼我們不把參數初始化成全0,那我們該初始化成什麼呢?換句話說,如何既保證輸入輸出的差異性,又能讓model穩定而快速的收斂呢?
要描述「差異性」,首先就能想到概率統計中的方差這個基本統計量。對於每個神經元的輸入z這個隨機變量,根據前面講BP時的公式,它是由線性映射函數得到的,
也就是 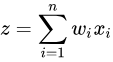 ,其中n是上一層神經元的數量。因此,根據概率統計裏的兩個隨機變量乘積的方差展開式:
,其中n是上一層神經元的數量。因此,根據概率統計裏的兩個隨機變量乘積的方差展開式:
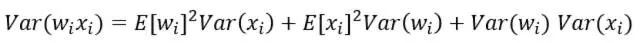
可以得到,如果E(xi)=E(wi)=0(可以通過批量歸一化Batch Normalization來滿足,其他大部分情況也不會差太多),那麼就有:
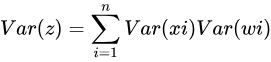
如果隨機變量xi和wi再滿足獨立同分布的話:
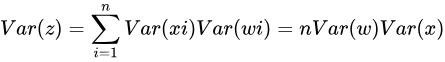
好了,這時重點來了。試想一下,根據文章《激活函數》,整個大型前饋神經網絡無非就是一個超級大映射,將原始樣本穩定的映射成它的類別。也就是將樣本空間映射到類別空間。試想,如果樣本空間與類別空間的分佈差異很大,比如說類別空間特別稠密,樣本空間特別稀疏遼闊,那麼在類別空間得到的用於反向傳播的誤差丟給樣本空間後簡直變得微不足道,也就是會導致模型的訓練非常緩慢。同樣,如果類別空間特別稀疏,樣本空間特別稠密,那麼在類別空間算出來的誤差丟給樣本空間後簡直是爆炸般的存在,即導致模型發散震盪,無法收斂。因此,我們要讓樣本空間與類別空間的分佈差異(密度差別)不要太大,也就是要讓它們的方差儘可能相等。
因此爲了得到Var(z)=Var(x),只能讓n*Var(w)=1,也就是Var(w)=1/n。
同樣的道理,正向傳播時是從前往後計算的,因此 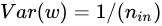 ,反向傳播時是從後往前計算的,因此
,反向傳播時是從後往前計算的,因此 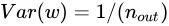 。然而
。然而 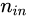 和
和 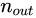 往往不相等啊,怎麼辦呢?所以就取他們的均值就好啦~即:
往往不相等啊,怎麼辦呢?所以就取他們的均值就好啦~即:
令 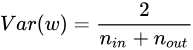
假設w爲均勻分佈的話,由w在區間[a,b]內均勻分佈時的方差爲
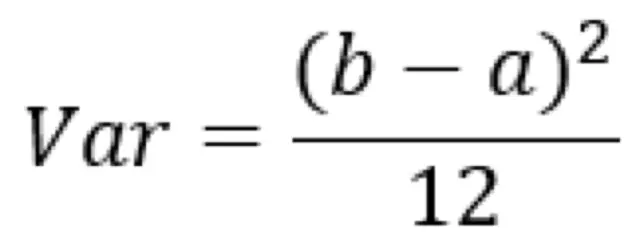
代碼前面的Var(w)公式解得參數a和b,即得:
![w\sim U[-\frac{\sqrt 6}{\sqrt {n_{in}+n_{out}}},\frac{\sqrt6}{\sqrt {n_{in}+n_{out}}}]](http://i2.bangqu.com/j/news/20180712/57E2pf153137163581752536.png)
(讓w在這個區間裏均勻採樣就好啦)
得到的這個結論就是Xavier初始化方法。這就是爲什麼使用Xavier初始化這個trick經常可以讓model的訓練速度和分類性能取得大幅提高啦~所以在使用前饋網絡時,除非你的網絡設計的明顯不滿足xavier的假設,否則使用xavier往往不會出錯。當然,另一方面來說,也很少有場合可以完全迎合xavier假設,因此時間充裕的話,改改分子,甚至去掉n_out都有可能帶來意想不到的效果。
參考文獻:Glorot X, Bengio Y. Understanding the difficulty of training deep feedforward neural networks[J]. Journal of Machine Learning Research, 2010, 9:249-256.
本文轉載自【夕小瑤的賣萌屋】,據說每個想學機器學習的人到這裏都停不下來了~