衆所周知，過參數化的深度神經網絡（DNN）是一類表達能力極強的函數，它們甚至可以以 100% 的訓練準確率記住隨機數據。這種現象就提出了一個問題：爲什麼它們不會輕易地過度擬合真實數據？爲了回答這個問題，我們使用傅立葉分析研究了深度神經網絡。我們證明了具有有限權重（或者經過有限步訓練）的深度神經網絡天然地偏向於在輸入空間上表示光滑的函數。具體而言，深度 ReLU 網絡函數的一個特定頻率分量（k）的大小至少以 O（k^(-2)）的速率衰減，網絡的寬度和深度分別以多項式和指數級別幫助網絡對更高的頻率建模。這就說明了爲什麼深度神經網絡不能完全記住 delta 型的峯函數。我們的研究還表明深度神經網絡可以利用低維數據流形的幾何結構來用簡單的函數逼近輸入空間中存在於簡單函數流形上的複雜函數。結果表明，被網絡分類爲屬於某個類的所有樣本（包括對抗性樣本）都可以通過一條路徑連接起來，這樣沿着該路徑上的網絡預測結果就不會改變。最後，我們發現對應於高頻分量的深度神經網絡（DNN）參數在參數空間中所佔的體積較小。
如今，人們已經做出了許多關於深度神經網絡表達能力的理論研究（Hornik et al., 1989; Cybenko, 1989; Montufar et al., 2014; Poole et al., 2016）。最近的研究表明，深度神經網絡（DNN）實際上能夠以 100% 的訓練準確率記憶隨機數據，這表明它們在過參數化的機制中確實有很強的表達能力（Zhang et al., 2017）。這大大激發了人們對深度學習的另一個領域（泛化理論）進行研究的興趣，從而理解爲什麼實際上的表現如此優秀，因爲能夠記住隨機數據的過參數化的神經網絡會使傳統的泛化邊界（例如，VC 維、Rademacher 複雜度等）變得無意義。在這些研究中，一個路線將目光投向了研究深度神經網絡（DNN）泛化問題的新方法（Neyshabur et al., 2015, 2017; Dziugaite and Roy, 2017）；另一個路線則研究基於隨機梯度下降（SGD）的方法如何在尋找最小值的問題中作爲隱式正則項提升泛化能力（Mandt et al., 2017; Chaudhari and Soatto, 2017; Jastrz˛ebski et al., 2017; Smith and Le, 2017）。
基於這些研究，研究者注意到過參數化的深度神經網絡（DNN）在訓練過程中優先學習簡單（或光滑）的函數，從而捕獲到數據中出現的全局性結構而不是過度擬合單個樣本（Arpit et al., 2017; Advani and Saxe, 2017）。有趣的是，這種現象已經被證明無論是在真實數據或是隨機生成的數據上都是成立的（Arpit et al., 2017）。因此，儘管這樣的深度神經網絡（DNN）是過參數化的並且具有很強的表達能力，它們似乎更偏向於擬合光滑函數。這也暗示着表徵這些函數的參數空間的容量很大。在本文中，研究者使用傅立葉分析來展示深度神經網絡（DNN）天然地就偏向於擬合光滑函數，而不是研究泛化問題或深度神經網絡優化方法的行爲。據作者所知，這是首次使用傅立葉分析研究深度神經網絡的工作。本文的貢獻如下：
本文展示了對於參數 θ 的任意有限值來說，深度神經網絡（DNN）的 ReLU 函數的一個特定的頻率分量（k）的量級至少以 O(1/k^2 ) 的速率衰減，並且網絡的寬度和深度分別以多項式和指數的級別幫助其捕獲更高的頻率；因此，高頻分量的大小會更小（DNN 更容易趨向於光滑）。其結果是，對深度神經網絡（DNN）進行有限步訓練使其更趨向於表示如上面所描述的函數。
作爲這一理論的附帶結果，研究者揭示了（有限權重）深度神經網絡在學習類似狄拉克 delta 函數（單位脈衝函數）峯函數的理論極限。這是因爲它的傅立葉變換的量級是一個常值函數（因此所有的頻率都有相同的振幅）。並且如上文中所討論的，深度神經網絡（DNN）無法學習對這樣的函數建模，因爲它們的傅立葉係數必須至少以 1/k^2 的速率衰減（儘管增加寬度和深度可以分別以多項式級和指數級別幫助其捕獲更高的頻率）。
研究者指出，如果在低維流形上定義數據-目標函數的映射，深度神經網絡（DNN）可以利用流形的幾何結構來對函數取近似，這些函數沿着流形（其函數的頻率分量相對於其輸入空間較低）具有高頻分量。
通過分析實驗表明，對於一個在 CIFAR-10 數據集上訓練的深度神經網絡（DNN）來說，存在幾乎線性的路徑能夠連接所有的對抗性樣本，它們被分類成一個特定的類（比如「貓」）。對於所有真正類別爲「貓」的訓練樣本，所有的樣本也沿着這條路徑被分類成同一個類別——「貓」。研究者進一步展示了對於在 CIFAR-10 數據集上訓練的深度神經網絡（DNN）來說，所有同一個類別中的訓練樣本也通過同樣的方式連接起來。
實驗表明，與帶有高頻分量的函數相對應的深度神經網絡（DNN）在參數空間中所佔的體積更小。
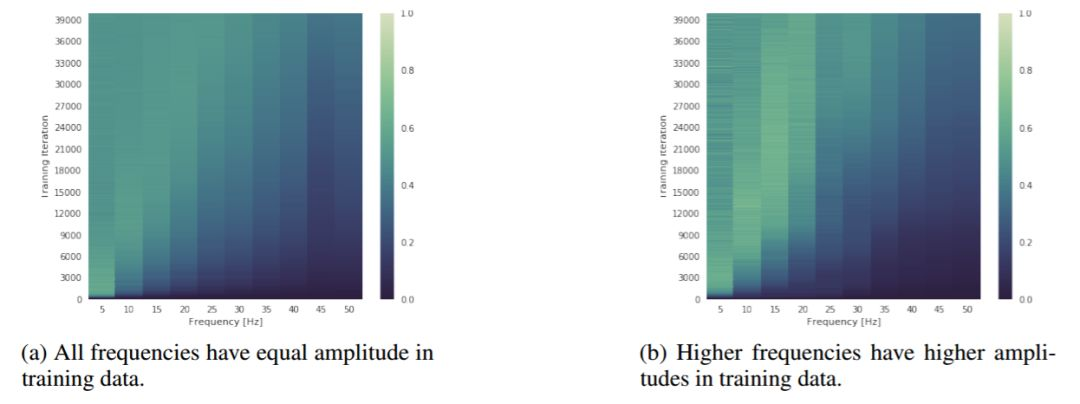圖 2：展示訓練期間（y 軸）頻譜演變（x 軸）的熱圖。顏色代表測量出的在相應的頻率上網絡頻譜的幅值，其值用相同的頻率的目標幅值進行了歸一化操作。此圖說明，儘管更高頻率的訓練數據具有 g 的振幅，深度神經網絡仍然優先訓練低頻數據。
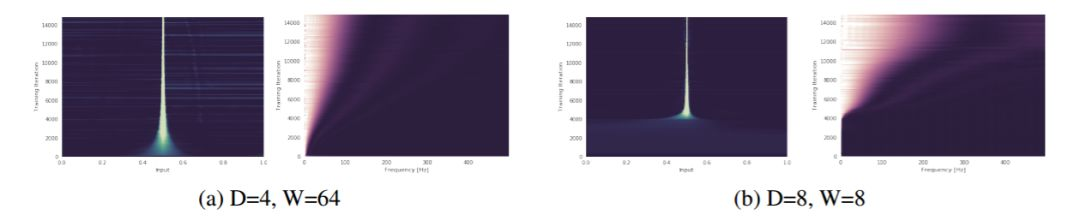圖 3: 一個深度爲 D、寬度爲 W，權重修剪 K=0.1 的網絡被訓練去預測一個 delta 峯（所有頻率的振幅都相同）。在圖（a）和圖（b）中，y 軸對應於不斷增加的訓練迭代次數（向上遞增），x 軸則代表頻域（右圖）和輸入域（左圖）。更亮的顏色表示數值更大。此圖說明，根據理論所闡述的，寬度和深度分別以多項式和指數級幫助網絡捕獲高頻分量。這一點在輸入域和頻域上都可以看出來（注：64^4=8^8）。更多的圖片請參見附錄（圖 11）。
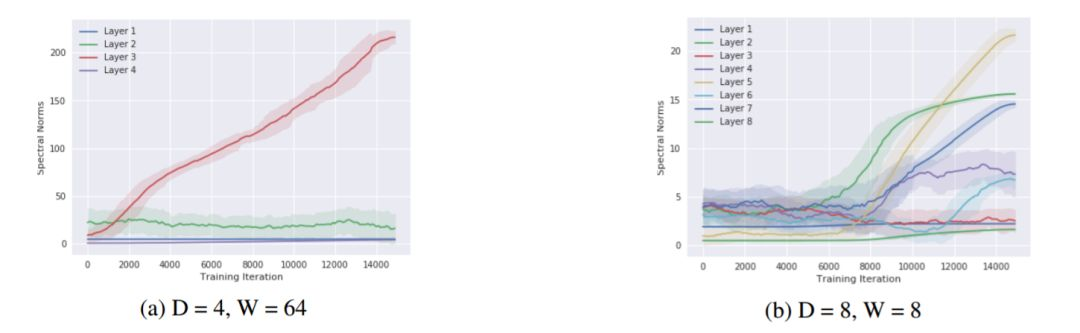圖 5: 在圖 3 中所使用的 delta 峯數據集上，一個深度爲 D 層、寬度爲 W 個單元的網絡的所有權重的譜範數（y 軸）與訓練過程中迭代次數（x 軸）的關係圖。
對於矩陣值權重，它們的譜範數是通過估計由 10 次冪迭代得到的特徵向量的特徵值計算而來。對於向量值權重，則僅使用了 L2 範數。此圖說明，隨着神經網絡通過學習去擬合更大的頻率，神經網絡權值的譜範數也增大，從而鬆弛頻譜的邊界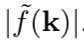
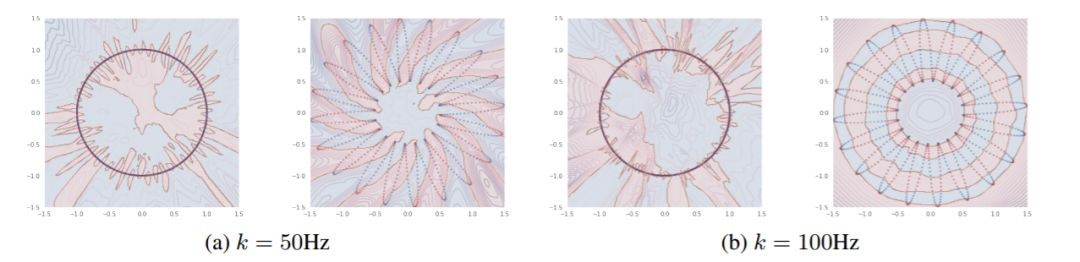圖 6: 在圖（a）和圖（b）中，左圖：L=0 瓣（虛線圓）；右圖：L=20 瓣（由 20 瓣組成的虛線花）定義了數據的流形。
對於這兩個流形，我們沿着流形定義了一個頻率爲 k Hz 的正弦信號，並將它二值化，得到一個 0/1 的目標（點的顏色）。對於每種情況，研究者訓練了一個 6 層深的 ReLU 網絡，將數據樣本從流形映射到它相應的目標上。填充的顏色表示預測出的類，等高線表示該網絡經過 sigmoid 函數處理的對數 logits 的絕對值。此圖說明，對應較大的 L 的流形，即使在兩種流形沿着流形的目標頻率相同時，也能使深度神經網絡在其域空間學習到更光滑的函數。可以看到，網絡會學習利用 L 值較大的流形的幾何結構去學習關於其輸入空間的低頻函數。這個結論在另一個實驗中得到了證實。
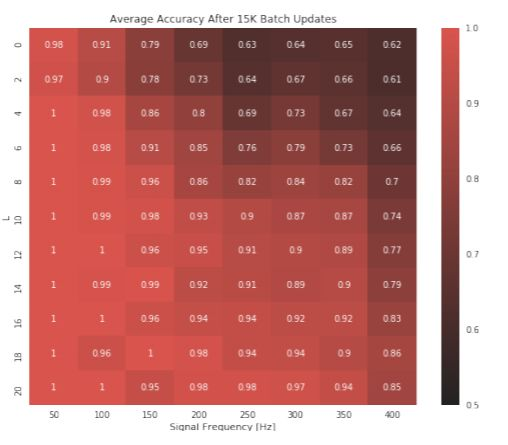圖 8: 用於預測定義在一個 L 瓣的流形（y 軸）上的給定頻率（x 軸）的二值化正弦波的訓練分類準確率的熱圖。此圖說明，如果目標信號的頻率較低或數據定義在一個具有更大的 L 的流形上，固定大小的網絡的準確率越高。後者的結果表明，隨着流形中瓣數的增加，在一個流形上學習一個高頻目標就變得更容易。
圖 9: 每一行都展示了圖像空間中的一條路徑，從右至左顯示了從對抗性樣本變爲一個真實訓練圖像的過程。
所有的圖像都被一個 ResNet-20 以不少於 95% 的 softmax 概率分類爲右側所示的訓練樣本的類別。本實驗表明，我們可以找到一條路徑，分類爲某一個特定類別（「飛機」）的對抗性樣本（右側，例如「貓」）與真實的訓練樣本類別（左側，「飛機」）相連，這樣以來沿着這條路徑的左右樣本都會被網絡預測爲同一個類別（「貓」）。
論文：On the Spectral Bias of Deep Neural Networks
論文鏈接：https://arxiv.org/pdf/1806.08734.pdf
摘要：衆所周知，過參數化的深度神經網絡（DNN）是一類表達能力極強的函數，它們甚至可以以 100% 的訓練準確率記住隨機數據。這種現象就提出了一個問題：爲什麼它們不會輕易地過度擬合真實數據？爲了回答這個問題，我們使用傅立葉分析研究了深度神經網絡。我們證明了具有有限權重（或者經過有限步訓練）的深度神經網絡天然地偏向於在輸入空間上表示光滑的函數。具體而言，深度 ReLU 網絡函數的一個特定頻率分量（k）的大小至少以 O（k^(-2)）的速率衰減，網絡的寬度和深度分別以多項式和指數級別幫助網絡對更高的頻率建模。這就說明了爲什麼深度神經網絡不能完全記住 delta 型的峯函數。我們的研究還表明深度神經網絡可以利用低維數據流形的幾何結構來用簡單的函數逼近輸入空間中存在於簡單函數流形上的複雜函數。結果表明，被網絡分類爲屬於某個類的所有樣本（包括對抗性樣本）都可以通過一條路徑連接起來，這樣沿着該路徑上的網絡預測結果就不會改變。最後，我們發現對應於高頻分量的深度神經網絡（DNN）參數在參數空間中所佔的體積較小。