一直以來，我們都不知道爲什麼深度神經網絡的損失能降到零，降到零不代表着全局最優了麼？這不是和一般 SGD 找到的都是局部極小點相矛盾麼？最近 CMU、清華和 MIT 的研究者分析了深層全連接網絡和殘差網絡，並表示使用梯度下降訓練過參數化的深度神經網絡真的能找到全局最優解。
用一階方法訓練的神經網絡已經對很多應用產生了顯著影響，但其理論特性卻依然是個謎。一個經驗觀察是，即使優化目標函數是非凸和非平滑的，隨機初始化的一階方法（如隨機梯度下降）仍然可以找到全局最小值（訓練損失接近爲零），這是訓練中的第一個神祕現象。令人驚訝的是，這個特性與標籤無關。在 Zhang 等人的論文 [2016] 中，作者用隨機生成的標籤取代了真正的標籤，但仍發現隨機初始化的一階方法總能達到零訓練損失。
人們普遍認爲過參數化是導致該現象的主要原因，因爲神經網絡只有具備足夠大的容量時才能擬合所有訓練數據。實際上，很多神經網絡架構都高度過參數化。例如，寬殘差網絡（Wide Residual Network）的參數量是訓練數據的 100 倍。
訓練深度神經網絡的第二個神祕現象是「更深的網絡更難訓練。」爲了解決這個問題，何愷明等人在 2006 年提出了深度殘差網絡（ResNet）架構，用隨機梯度下降方法來訓練顯著具有更多層數的神經網絡。理論上來說，Hardt 和 Ma [2016] 表明，線性網絡中的殘差連接可以阻止梯度消失爲零，但使用非線性激活函數的神經網絡還無法利用殘差連接的優勢。
在本文中，作者將揭開這兩個神祕現象的面紗。具體而言，作者們從理論上分析了損失函數在梯度下降上的收斂情況，即採用全連接網絡和殘差網絡架構下的損失函數收斂情況。作者關注根據歐式距離定義的損失函數，並假設激活函數是 Lipschitz 和平滑的。這種假設適用於很多激活函數，包括 soft-plus。本文貢獻如下：
首先考慮全連接前饋網絡。作者表明，如果層級的神經元數量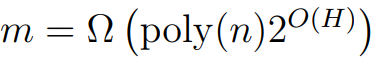
，則隨機初始化的梯度下降會以線性速率收斂到零訓練損失。
接下來考慮 ResNet 架構。作者表明，只要中間層的寬度 m = Ω (poly(n, H))，則隨機初始化的梯度下降會以線性速率收斂到零訓練損失。與第一個結果相比，ResNet 對網絡層數的依賴呈指數級上升。該理論闡明瞭利用殘差連接的優勢。
最後，作者利用同樣的技術來分析卷積 ResNet。作者表明，如果 m = poly(n, p, H)，其中 p 是圖像塊數量，則隨機初始化的梯度下降會達到零訓練損失。
本文的證明是基於以前關於雙層神經網絡梯度下降研究中的兩個重要概念。第一個是 Du 等人 [2018b] 提出的概念，本文作者分析了神經網絡預測的動力學特徵，即其收斂性由格拉姆矩陣（Gram matrix）的最小特徵值決定。爲了降低最小特徵值的下界，從初始化開始限制每個權重矩陣的距離就足夠了。其次，作者利用了 Li 和 Liang [2018] 的觀察結果，即如果神經網絡過參數化，則每個權重矩陣接近其初始化。與前兩個研究不同，本文在分析深度神經網絡時，需要構建更多深度神經網絡的架構屬性和新技術。在本文中，我們主要介紹了 ResNet 的分析結果，更詳細的證明展示在原論文中的 29 頁附錄中。
論文：Gradient Descent Finds Global Minima of Deep Neural Networks
論文地址：https://arxiv.org/pdf/1811.03804.pdf
摘要：在訓練深度神經網絡時，即使目標函數是非凸的，梯度下降法也能找到全局最小值。本文證明了對於具有殘差連接的深度超參數神經網絡（ResNet），梯度下降可以在多項式時間內實現零訓練損失。我們的分析依賴於神經網絡架構引入的格拉姆矩陣的多項式結構。這種結構幫助我們證明格拉姆矩陣在訓練過程中的穩定性，而且這種穩定性意味着梯度下降算法的全局最優性。我們的邊界也揭示了使用 ResNet 優於全連接前饋架構的優點；對於前饋網絡，我們的邊界要求每層神經元的數量隨深度進行指數縮放，而對於 ResNet，邊界只要求每層神經元的數量隨深度進行多項式縮放。我們還進一步將自己的分析擴展到深度殘差卷積神經網絡並得到了類似的收斂結果。
本文結構：第二節正式介紹了問題背景；第三節給出了在深度全連接神經網絡上得到的主要結果；第四節給出了在 ResNet 上得到的主要結果；第五節給出了在卷積 ResNet 上得到的主要結果；第六節爲以上三種架構提供了一個統一的證明策略。第 7 節爲總結，證明見附錄。
在論文的後面的章節中，大部分都在描述假設與推理。尤其在後面 29 頁的附錄中，作者給出了各推理的完整的證明。如果讀者自信數學底子比較硬朗的話，可以查閱原論文了解詳細推導過程，本文後面只簡要介紹了 ResNet 的分析結果。
ResNet 的主要分析結果
在這一章節中，作者主要會考慮使用梯度下降訓練 ResNet 的收斂性，並關注到底需要多大程度的過參數化才能確保梯度下降收斂到全局最優解。當然在這之前需要明確 ResNet 的形式化定義是什麼樣的。在這篇論文中，作者們主要分析了不同神經網絡的經驗風險最小化問題，其中損失函數由一般的歐式距離定義：
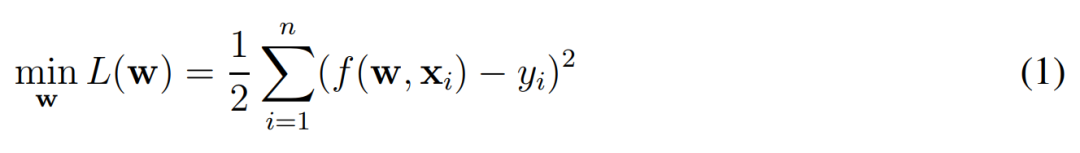
這個式子很容易理解，w 是神經網絡所有的權重，x 爲輸入樣本（如圖像）、y 爲樣本的對應標註。在實踐中，f(w, x_i) 表示的就是一個完整的殘差網絡（ResNet），我們希望利用梯度下降一步步調整 ResNet 中的權重 w，進而獲得經過訓練的 ResNet。從形式化上來說，ResNet 或 f(w, x_i) 函數可以表示爲如下方程式：
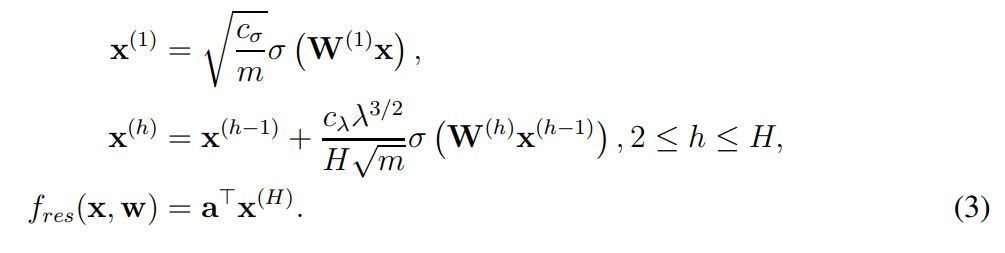
其中 x^(1) 表示輸入圖像 x 經第一個卷積層得出的特徵圖（feature map），c_σ爲初始化階段中歸一化輸入的縮放因子，這裏並沒有詳細展示 c_σ的表達式，詳情可查看原論文。此外，σ表示一般的激活函數，且作者假設算出來的中間層（x）都是方陣。在 x^(h) 中，作者形式化定義了殘差第 h 個殘差模塊的輸出，它會通過殘差連接將 h-1 層的輸出加上當前層的輸出。x^(h) 後面σ左邊比較複雜的表達式展示了這一層級的縮放因子，它們具體是什麼可以查閱原論文。
最後的 f_res(x, w) 則表示了殘差網絡的最終表達式，即最後一個殘差模塊的輸出做一個簡單的反射變換。因此爲了分析 ResNet 的收斂情況，作者定義了總體格萊姆矩陣，即對於所有 (i, j) ∈ [n] × [n]，我們有：
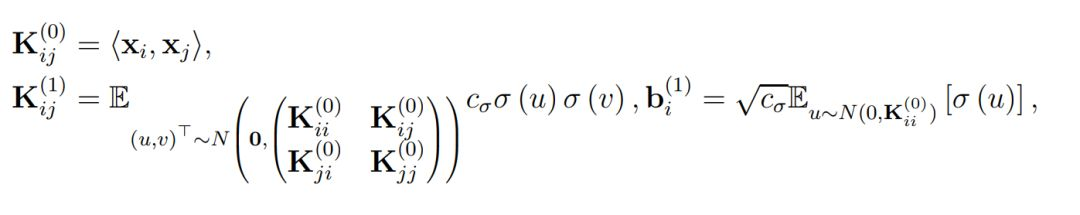
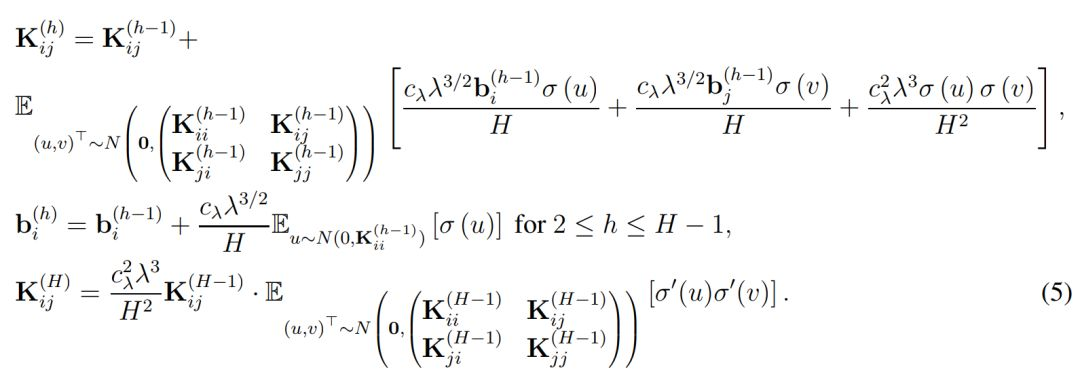
直觀上而言，K^(h) 表示了在經過複合 h 次核函數後所得到的格萊姆矩陣（Gram matrix），其中核函數都是由激活函數σ所定義。此外，當權重矩陣的長和寬 m 趨向於無窮大時，它們會漸進格萊姆矩陣。因此作者做了以下假設以決定收斂率和過參數化總量：
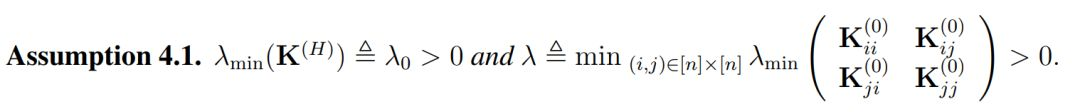
注意 λ 在這裏僅依賴於 K^(0)，因此它的定義與全連接網絡中的不太一樣。一般而言，除非兩個數據點是平行的，否則λ通常都是正數。在有了這個假設以後，作者給出了他們對 ResNet 的主要定理：
與全連接網絡中得出的定理不同，定理 4.1 完全是多項式形式的，因爲神經元數量和收斂率都是關於 n 和 H 的多項式，所以作者根據分析結果表明經典多層全連接架構和 ResNet 架構是有顯著差別的。作者在這裏並沒有使用任何指數因子，其主要原因是殘差連接塊使得整個架構在初始化階段和訓練階段都更加穩定。
以上只是 ResNet 分析所獲得的結果，更多分析和推導過程都在原論文中。作者最後表示過參數化網絡上實現的梯度下降能獲得零訓練損失，且證明的關鍵技術是表明格萊姆矩陣在過參數化的情況下會越來越穩定，因此下降的每一步都會以幾何速率減少損失，並最終收斂到全局最優解。