深度學習已經成熟到可以教給高中生了麼？
我思考的這個問題，源於不久前我收到的⼀封來自某大公司產品經理的郵件。
我喜歡將私人通訊郵件公開於衆，所以我將郵件內容摘在下面：
來自:M.
你好 Ali, ...
你如何訓練團隊裏的年輕成員，使得他們有更好的直覺和預判？我團隊裏的工程師經常從其他科研⼈員那「借鑑」超參數的值，但他們太擔心要自己去調整參數了。...
我對着這封郵件思考了數日，卻沒有辦法找到⼀個有條理的答案。
如果說應該有正確答案的話，我想回復說：也許她的工程師應該要有這種擔心。
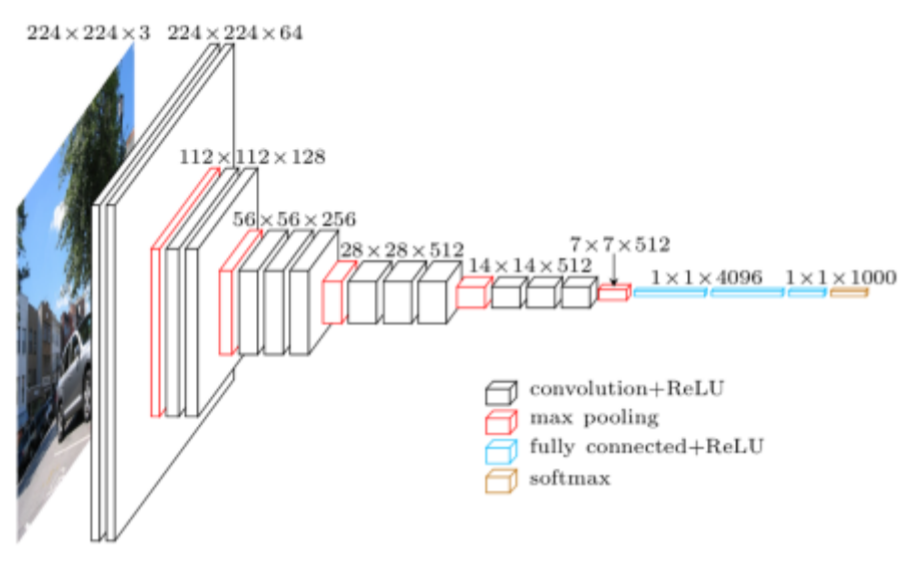
如果你是⼀個工程師，你拿到了這個神經網絡，然後你被要求去改進這個網絡在某個數據集上的表現。你也許會假設這每⼀層都是有它自己的作用和功能，但在深度學習領域，我們目前還沒有統⼀的語言和詞彙去描述這些功效。我們教授深度學習的方法和我們教授其他科學學科的方法很不同。
幾年前我迷上了光學。在光學領域，你會堆疊好幾層不同的組件以處理輸⼊的光源。例如下圖，就是相機的鏡頭：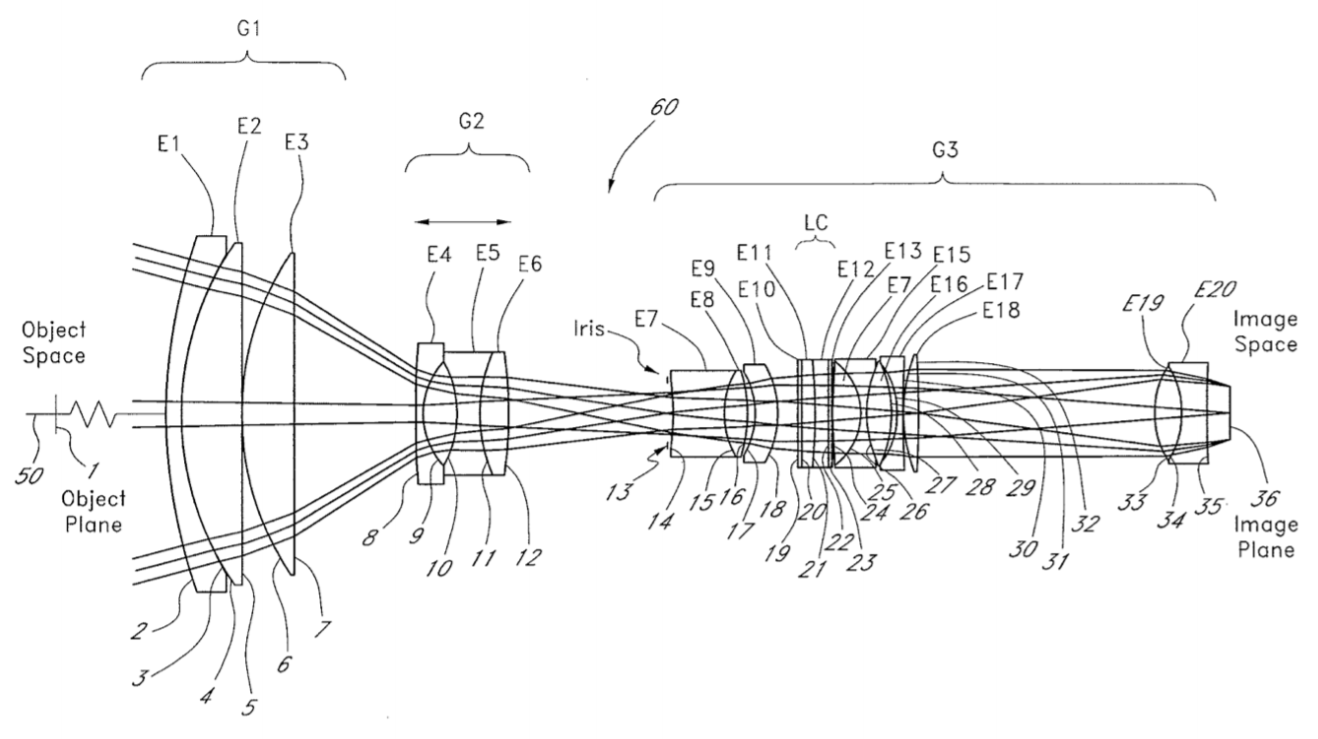 
要設計這樣的系統，你從最簡單的組件開始堆疊，這些組件往往以知名的發明者命名。然後通過仿真，你可 以判斷你的設計是否符合你的要求，然後再添加不同的組件去修正先前設計的缺陷。
緊接着你會各種數學優化過程去調整這些組件的參數，例如鏡面的形狀、位置和傾斜角度等等，去最大程度實現你的設計目標。你就重複如此仿真、修改、調優的過程。
這很像我們設計深度網絡的過程。
上圖裏所有的 36 個元素都是故意加⼊這個堆疊的系統，以用於修正某項具體的偏差的。這樣的設計需要非常精確的解釋模型去描述什麼樣的元素能夠對透過它的光有什麼樣的效應。這個模型往往是關於這個元素的作用的，例如說折射、反射、衍射、散射和波前校正。
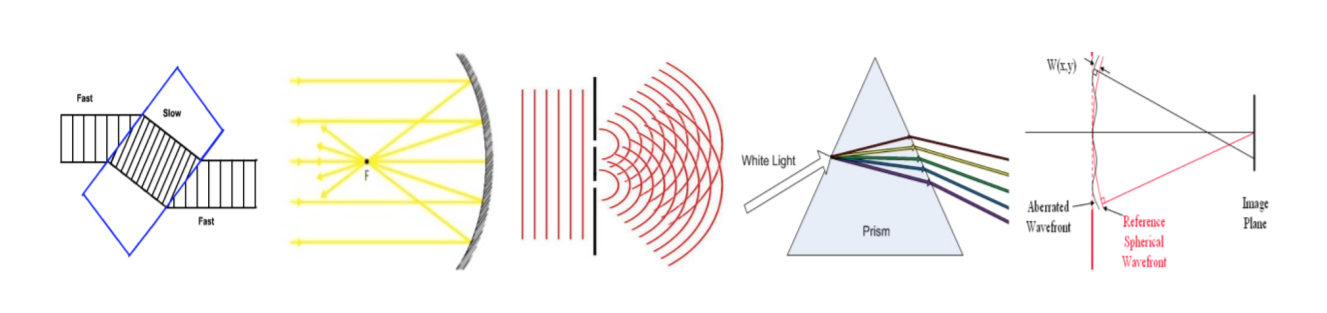⼈們不害怕這樣的設計過程。每年，美國培養的許多⼯程師都能設計出有⽤的鏡頭，他們並不爲這樣的⼯作 感到擔心害怕。
這並不是因爲光學很容易，而是因爲我們對光學的模型瞭然在心。
現代光學是通過抽象出不同層級的知識內容去教授的。
在最頂級，也是最容易的層級，是幾何光學。幾何光學是對波光學的抽象，光射線于于表達簡單的矢量波光 學的波前矢量。而波光學⼜是對麥克斯韋方程的進⼀步簡化。麥克斯韋方程 由能由量子力學推導而出，量子力學則超出了我的理解範圍。
每⼀個層級都是通過作出⼀些簡化的假定由緊鄰的下⼀個層級推導⽽出，所以每⼀個層級能夠比上⼀個層級解釋更爲複雜的現象。
我花了不少時間在頂四層抽象裏設計系統。
這就是當今我們教授光學的方法。但相關理論並非總是如此按層級來組織。在百年前，這些理論還是在⼀個 相互矛盾的狀態中共存。實踐家們只能依賴於近乎道聽途說的光學理論。
但這並沒有阻止伽利略打造性能不錯的望遠鏡，而且是在牛頓形式化幾何光學前近⼀個世紀的時間點上。因 爲伽利略對於如何造出能夠放大數⼗倍的望遠鏡有足夠好的解釋模型。但他對光學的理解，卻不足以讓他的望遠鏡能夠修正色差或者獲得廣視角。
在這些光學理論被抽象總結出來之前，每⼀項理論都需要從光的最基本概念出發。這就牽涉到要作出⼀套涵蓋許多也許不切實際的假設。牛頓的幾何光學把光假定作⼀束束可以被吸引、排斥的固體粒⼦。惠更斯則⽤ 由「以太」作爲介質的縱波去描述光，也就是說用類似聲波的方式去構建光。麥克斯韋也假設光經由以太傳播。你從麥克斯韋方程的係數的名字也能窺得這種思路的⼀⼆。
愚蠢的模型，確實。但它們可量化且有預測的能力。
這些假設，我們今天聽來也許覺得很愚蠢，但它們可量化而且有預測的能力。你可以隨意代入數字於其中並得到精準的量化預測。這對於工程師而言極其有用。
尋找用於描述每⼀層深度學習網絡作用的模塊化語言
如果我們能夠像討論光纖穿越每⼀層鏡頭元素的作用那樣去討論神經網絡每⼀層的作用，那麼設計神經網絡將會變得更容易。
我們說卷積層就像在輸⼊上滑動相應濾波器，然後說池化是處理了對應的非線性。但這只是非常低層次的描述，就像用麥克斯韋方程去解釋鏡頭的作用。
也許我們應該依賴於更高級抽象描述，具體表達某個量被神經網絡的層級如何改變了，好比我們用鏡頭的具 體作用去解釋它如何彎曲光線那樣。
如果這種抽象也能夠量化，使得你只需要代⼊具體數值到某個公式裏，它就能告訴你⼀個大概的量化分析，這樣你就能更好地設計你的網絡了。
我們離這樣的語言還很遠。我們先從簡單點的開始
上⾯也許只是我被自己的幻想帶跑了。
我們從簡單點的開始。我們對深度學習的運作方式有很多解釋模型。下⾯我會羅列⼀系列值得解釋的現象，然後我們看看⼀些現有的模型對這些現象解釋的能力有多強。
在開始之前，我得承認這種努力也許最後是徒勞的。光學花了 300 年在打磨自己的模型之上，而我只花了⼀ 個週六下午，所以這隻能算是博客上的⼀些個⼈觀點和想法。
現象：隨機梯度下降 (SGD) 的隨機初始化足夠好了。但細微的數字錯誤或者步長會使 SGD 失效。
很多⼈在實踐中發現，對於如何累積梯度的細微調整，可以導致對整個測試集表現的巨大變化。例如說你只用GPU而不是 CPU 去訓練，結果可能會截然不同。
現象：淺的局部最優值意味着比深的局部最優值更好的泛化能力。
這種說法很時髦。有些⼈認爲它是真的。有些⼈則用實際數據反駁。另外也有⼈給出了這個現象的變種 。衆說紛紜，爭議目前不斷。
這個現象也許有爭議性，但我還是先放在這裏。
現象：批標準化層 (Batch Norm) 可以給 SGD 提速。
這個基本無爭議，我只能提供⼀個小例外。
現象：即使有很多局部最優和鞍點，SGD 也表現卓越。
這個說法也包含了幾個小的點。經常有人聲稱深度學習的損失表面充斥着鞍點和局部最優。也有不同的 說法，要不就認爲梯度下降可以遍歷這些區域，要不就認爲梯度下降可以不遍歷這些區域，但都能給出泛化能力不錯的答案。也有說損失表面其實也沒那麼不堪。
現象：Dropout 勝於其他隨機化策略。
我不知道如何正確分類類似 Dropout 的做法，所以我就稱之爲「隨機化策略」了。
現象：深度網絡能夠記憶隨機標籤，但它們能泛化。
證據很直白，我的朋友們親自見證並主張這種說法。
對這些現象的解釋
對應上面列舉的這些現象，我在下面列舉我覺得最能解釋這些現象的理論，這些理論均來自我上面引用的論文。
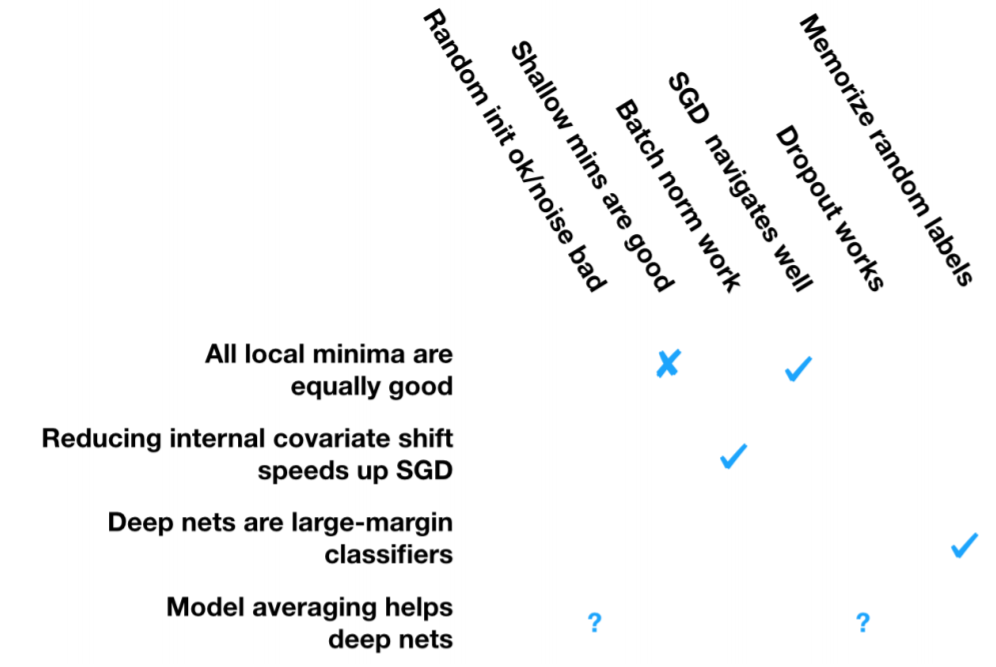先別激動，原因如下：
1. 我們嘗試解釋的這些現象部分有爭議。
2. 我沒辦法把這些解釋按照抽象層級組織好。光學好教學的特性也沒辦法在這⾥重現。
3. 我懷疑部分我引用的理論不正確。
我想說的是
有很多人正在加⼊這個領域，然而我們能夠給他們傳授的不過是近乎道聽途說的經驗和⼀些預訓練好的深度網絡，然後就叫他們去繼續創新。我們甚⾄都不能認同我們要解釋的這些現象。所以我認爲我們離能夠在高中教授這些內容還有很遠的距離。
那我們如何才能離這⼀步近點？
最好的不過是我們能夠就每⼀層深度網絡的功能作用，按照不同層級的抽象，給出對應的解釋模型。例如 說，神經網絡裏的折射、散射和衍射會是怎麼樣的？也許你早就用具體的功能去思考神經網絡，但我們就這些概念還沒有統⼀的語言。
我們應該把⼀系列確認的現象組織起來，然後纔來進行理論上的解釋。例如說神經網絡裏的牛頓環、磁光克 爾效應和法拉第現象會是怎樣的？
我和一小批同事已經開始了⼀項重大的實踐工作，嘗試去分類構建適合我們領域的解釋模型，去形式化它 們，並且用實驗去驗證它們。這項工作是巨大的，我認爲第⼀步應該是構建⼀個分層級的深度學習解釋模 型，以用於高中的教學。
原文鏈接：http://www.argmin.net/2018/01/25/optics/